Problem:
Triangle with and has area 120 . Let be the midpoint of , and let be the midpoint of . The angle bisector of intersects and at and , respectively. What is the area of quadrilateral
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Because is of , it follows from the Angle Bisector Theorem that is of , and is of . Because trapezoids and have the same height, the area of is of the area of . Furthermore, the area of is of the area of , so its area is 30 , and the area of trapezoid is . Therefore the area of quadrilateral is .
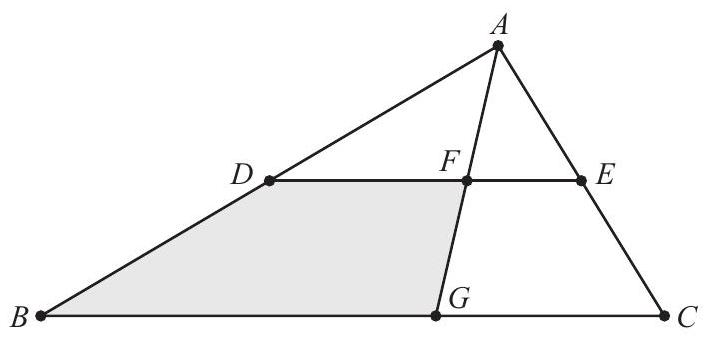
Note: The figure (not drawn to scale) shows the situation in which is acute. In this case and . It is also possible for to be obtuse, with and . These values can be calculated using the Law of Cosines and the sine formula for area.
The problems on this page are the property of the MAA's American Mathematics Competitions