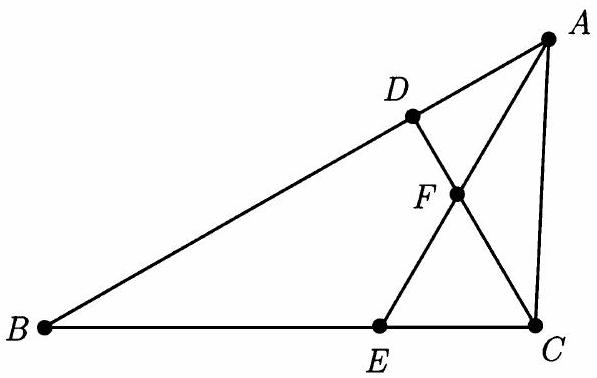
Problem:
Triangle ABC has AB=2⋅AC. Let D and E be on AB and BC, respectively, such that ∠BAE=∠ACD. Let F be the intersection of segments AE and CD, and suppose that △CFE is equilateral. What is ∠ACB?
Answer Choices:
A. 60∘
B. 75∘
C. 90∘
D. 105∘
E. 120∘
Solution:
Let α=∠BAE=∠ACD=∠ACF. Because △CFE is equilateral, it follows that ∠CFA=120∘ and then
∠FAC=180∘−120∘−∠ACF=60∘−α.
Therefore
∠BAC=∠BAE+∠FAC=α+(60∘−α)=60∘
Because AB=2⋅AC, it follows that △BAC is a 30−60−90∘ triangle, and thus ∠ACB=90∘.
The problems on this page are the property of the MAA's American Mathematics Competitions