Problem:
How many unordered pairs of edges of a given cube determine a plane?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Without loss of generality, choose one of the edges of the cube to be among the two selected. We now calculate the probability that a randomly selected second edge makes the pair satisfy the condition in the problem statement.
For two lines in space to determine a common plane, they must either intersect or be parallel (in other words, they cannot be skew lines). If all line segments are extended to lines, the first (arbitrarily chosen) edge's line intersects lines and is parallel to another . Thus of the remaining line segments (which could be chosen for the second edge) give a pair of lines determining a common plane. To see this, observe that in the diagram below, the red edge is parallel to the green edges and intersects with the blue edges.
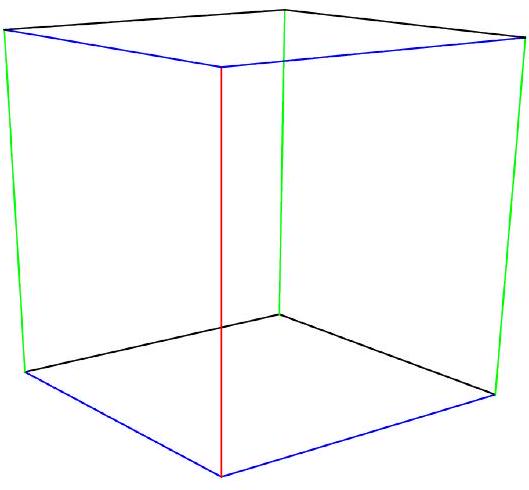
This means that the probability that a randomly-selected pair of edges determine a plane is , and we calculate that there are total pairs of edges that could be chosen (without the restriction). Thus the answer is .
OR
As in Solution , we observe that the two edges must either be parallel or intersect. Clearly the edges will intersect if and only if they are part of the same face. We can thus divide into two cases:
Case : The two edges are part of the same face. There are 6 faces, and ways to choose of the edges of the square, giving a total of possibilities.
Case : The two edges are parallel and not part of the same face. Observe that each of the edges is parallel to exactly edge that is not part of its face. The edges can thus be paired up, giving possibilities for this case.
Adding the two cases, the answer is hence .
The problems on this page are the property of the MAA's American Mathematics Competitions