Problem:
Eight congruent equilateral triangles, each of a different color, are used to construct a regular octahedron. How many distinguishable ways are there to construct the octahedron? (Two colored octahedrons are distinguishable if neither can be rotated to look just like the other.)
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The octahedron has 8 congruent equilateral triangular faces that form 4 pairs of parallel faces. Choose one color for the bottom face. There are 7 choices for the color of the top face. Three of the remaining faces have an edge in common with the bottom face. There are ways of choosing the colors for these faces and two ways to arrange these on the three faces (clockwise and counterclockwise). Finally, there are ways to fix the last three colors. Thus the total number of distinguishable octahedrons that can be constructed is .
OR
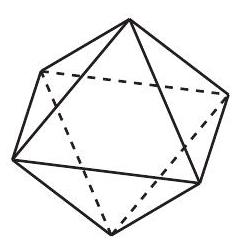
Place a cube inside the octahedron so that each of its vertices touches a face of the octahedron. Then assigning colors to the faces of the octahedron is equivalent to assigning colors to the vertices of the cube. Pick one vertex and assign it a color. Then the remaining colors can be assigned in 7! ways. Since three vertices are joined by edges to the first vertex, they are interchangeable by a rotation of the cube, hence the answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions