Problem: A ( 2 1 , 2 2 ) , B ( 2 3 , 2 4 ) A ( log 2 1 , log 2 2 ) , B ( log 2 3 , log 2 4 ) C ( 2 7 , 2 8 ) C ( log 2 7 , log 2 8 ) △ A B C △ A B C
Answer Choices:
A. 2 3 7 log 2 7 3
B. 2 3 7 log 2 7 3
C. 2 7 3 log 2 3 7
D. 2 11 7 log 2 7 1 1
E. 2 11 3 log 2 3 1 1
Solution:
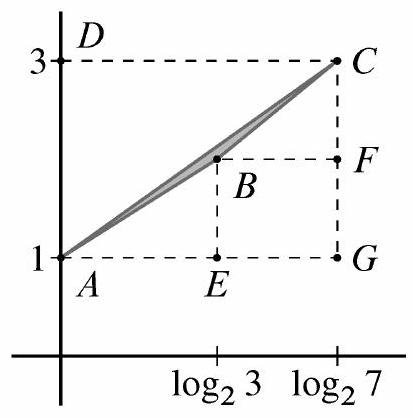
Circumscribe △ A B C △ A B C A G C D A G C D D D y y B B A G ‾ A G C G ‾ C G E E F F
The area of rectangle A G C D A G C D 2 2 7 2 log 2 7 △ A C G △ A C G 2 7 log 2 7
Area ( △ A B C ) = Area ( △ A C G ) − Area ( △ A B E ) − Area ( △ B C F ) − Area ( B E G F ) . A r e a ( △ A B C ) = A r e a ( △ A C G ) − A r e a ( △ A B E ) − A r e a ( △ B C F ) − A r e a ( B E G F ) .
Note that
Area ( △ A B E ) = 1 2 2 3 ⋅ 1 = 2 3 , Area ( △ B C F ) = 1 2 ( 2 7 − 2 3 ) ⋅ 1 = 2 7 3 , and Area ( B E G F ) = ( 2 7 − 2 3 ) ⋅ 1 = 2 7 3 . A r e a ( △ A B E ) = 2 1 log 2 3 ⋅ 1 = log 2 3 , A r e a ( △ B C F ) = 2 1 ( log 2 7 − log 2 3 ) ⋅ 1 = log 2 3 7 , and A r e a ( B E G F ) = ( log 2 7 − log 2 3 ) ⋅ 1 = log 2 3 7 .
Therefore
Area ( △ A B C ) = 2 7 − 2 3 − 2 7 3 − 2 7 3 = 2 ( 7 3 ⋅ 7 3 ⋅ 7 3 ) = ( B ) 2 3 7 . Area ( △ A B C ) = log 2 7 − log 2 3 − log 2 3 7 − log 2 3 7 = log 2 ⎝ ⎛ 3 ⋅ 3 7 ⋅ 3 7 7 ⎠ ⎞ = ( B ) log 2 7 3 .
OR OR
The area of triangle △ A B C △ A B C
1 2 det [ 1 0 1 1 2 3 2 1 2 7 3 ] = 1 2 det [ 1 0 1 − 1 2 3 0 − 2 2 7 0 ] = 1 2 det [ − 1 2 3 − 2 2 7 ] = 1 2 ( − 2 7 + 2 9 ) = 2 3 7 2 1 d e t ⎣ ⎢ ⎡ 1 1 1 0 log 2 3 log 2 7 1 2 3 ⎦ ⎥ ⎤ = 2 1 d e t ⎣ ⎢ ⎡ 1 − 1 − 2 0 log 2 3 log 2 7 1 0 0 ⎦ ⎥ ⎤ = 2 1 d e t [ − 1 − 2 log 2 3 log 2 7 ] = 2 1 ( − log 2 7 + log 2 9 ) = log 2 7 3
The cross product of two vectors in the x − y x − y z z A ( 0 , 1 , 0 ) , B ( 2 3 , 2 , 0 ) A ( 0 , 1 , 0 ) , B ( log 2 3 , 2 , 0 ) C ( 2 7 , 3 , 0 ) C ( log 2 7 , 3 , 0 ) z z
1 2 ( B − A ) × ( C − A ) = 1 2 ( 2 3 , 1 , 0 ) × ( 2 7 , 2 , 0 ) = 1 2 ( 1 ⋅ 0 − 0 ⋅ 2 , 2 7 ⋅ 0 − 2 3 ⋅ 0 , 2 3 ⋅ 2 − 1 ⋅ 2 7 ) = ( 0 , 0 , 2 3 − 2 7 ) = ( 0 , 0 , 2 3 7 ) . 2 1 ( B − A ) × ( C − A ) = 2 1 ( log 2 3 , 1 , 0 ) × ( log 2 7 , 2 , 0 ) = 2 1 ( 1 ⋅ 0 − 0 ⋅ 2 , log 2 7 ⋅ 0 − log 2 3 ⋅ 0 , log 2 3 ⋅ 2 − 1 ⋅ log 2 7 ) = ( 0 , 0 , log 2 3 − log 2 7 ) = ( 0 , 0 , log 2 7 3 ) .
Thus the area of the triangle is ( B ) 2 3 7 ( B ) log 2 7 3
OR OR
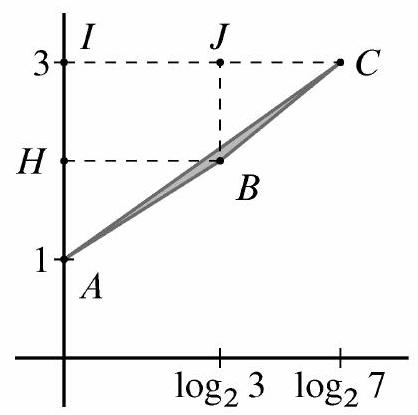
Define the points H ( 0 , 2 ) , I ( 0 , 3 ) H ( 0 , 2 ) , I ( 0 , 3 ) J ( 2 3 , 3 ) J ( log 2 3 , 3 )
Then H B C I H B C I △ C J B △ C J B
2 3 > 2 7 = 1 2 2 7 , log 2 3 > log 2 7 = 2 1 log 2 7 ,
point B B A C A C
Area ( △ A B C ) = Area ( △ A B H ) + Area ( H B C I ) − Area ( △ A C I ) = 1 2 2 3 + 1 2 ( 2 7 − 2 3 ) + 2 3 − 2 7 = 2 3 − 1 2 2 7 = ( B ) 2 3 7 . A r e a ( △ A B C ) = A r e a ( △ A B H ) + A r e a ( H B C I ) − A r e a ( △ A C I ) = 2 1 log 2 3 + 2 1 ( log 2 7 − log 2 3 ) + log 2 3 − log 2 7 = log 2 3 − 2 1 log 2 7 = ( B ) log 2 7 3 .
The problems on this page are the property of the MAA's American Mathematics Competitions