Problem:
Through a point on the hypotenuse of a right triangle, lines are drawn parallel to the legs of the triangle so that the triangle is divided into a square and two smaller right triangles. The area of one of the two small right triangle is times the area of the square. The ratio of the area of the other small right triangle to the area of the square is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
With out loss of generality, let the side of the square have length 1 unit and let the area of triangle be . Let and . Because triangles and are similar, . Since , the area of triangle is .
.jpg)
\section*{}
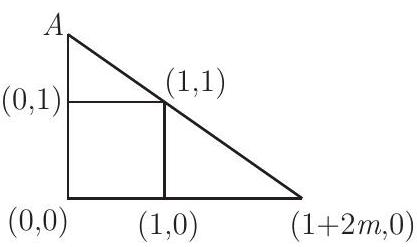
Let and be the vertices of the square. Let , and notice that the area of is 1 and the area of triangle is . The slope of the line through and is ; thus, it intersects the -axis at . The area of triangle is therefore .
The problems on this page are the property of the MAA's American Mathematics Competitions