Problem:
In triangle ABC,∠ABC=45∘. Point D is on BC so that 2⋅BD=CD and ∠DAB=15∘. Find ∠ACB.
Answer Choices:
A. 54∘
B. 60∘
C. 72∘
D. 75∘
E. 90∘
Solution:
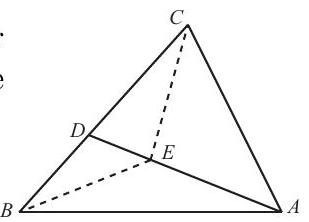
Let E be a point on AD such that CE is perpendicular to AD, and draw BE. Since ∠ADC is an exterior angle of △ADB it follows that
∠ADC=∠DAB+∠ABD=15∘+45∘=60∘.
Thus, △CDE is a 30∘−60∘−90∘ triangle and DE=21CD=BD. Hence, △BDE is isosceles and ∠EBD=∠BED=30∘. But ∠ECB is also equal to 30∘ and therefore △BEC is isosceles with BE=EC. On the other hand,
∠ABE=∠ABD−∠EBD=45∘−30∘=15∘=∠EAB.
Thus, △ABE is isosceles with AE=BE. Hence AE=BE=EC. The right triangle AEC is also isosceles with ∠EAC=∠ECA=45∘. Hence,
∠ACB=∠ECA+∠ECD=45∘+30∘=75∘.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)