Problem:
Let f(x)=x2+6x+1, and let R denote the set of points (x,y) in the coordinate plane such that
f(x)+f(y)≤0 and f(x)−f(y)≤0
The area of R is closest to
Answer Choices:
A. 21
B. 22
C. 23
D. 24
E. 25
Solution:
Note that
f(x)+f(y)=x2+6x+y2+6y+2=(x+3)2+(y+3)2−16
and
f(x)−f(y)=x2−y2+6(x−y)=(x−y)(x+y+6).
The given conditions can be written as
(x+3)2+(y+3)2≤16 and (x−y)(x+y+6)≤0
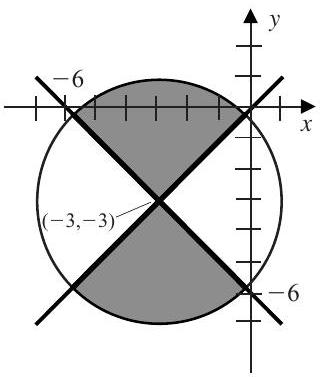
The first inequality describes the region on and inside the circle of radius 4 with center (−3,−3). The second inequality can be rewritten as
(x−y≥0 and x+y+6≤0) or (x−y≤0 and x+y+6≥0)
Each of these inequalities describes a half-plane bounded by a line that passes through (−3,−3) and has slope 1 or -1 . Thus, the set R is the shaded region in the following diagram, and its area is half the area of the circle, which is 8π≈25.13.
The problems on this page are the property of the MAA's American Mathematics Competitions