Problem:
Let be the set of circles in the coordinate plane that are tangent to each of the three circles with equations , and . What is the sum of the areas of all circles in ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Note that the given circles are centered at , and and have radii 2,8 , and , respectively. Label these circles , and , respectively. Let be a circle in . Then must be internally tangent to the circle of radius 8 . There are two cases.
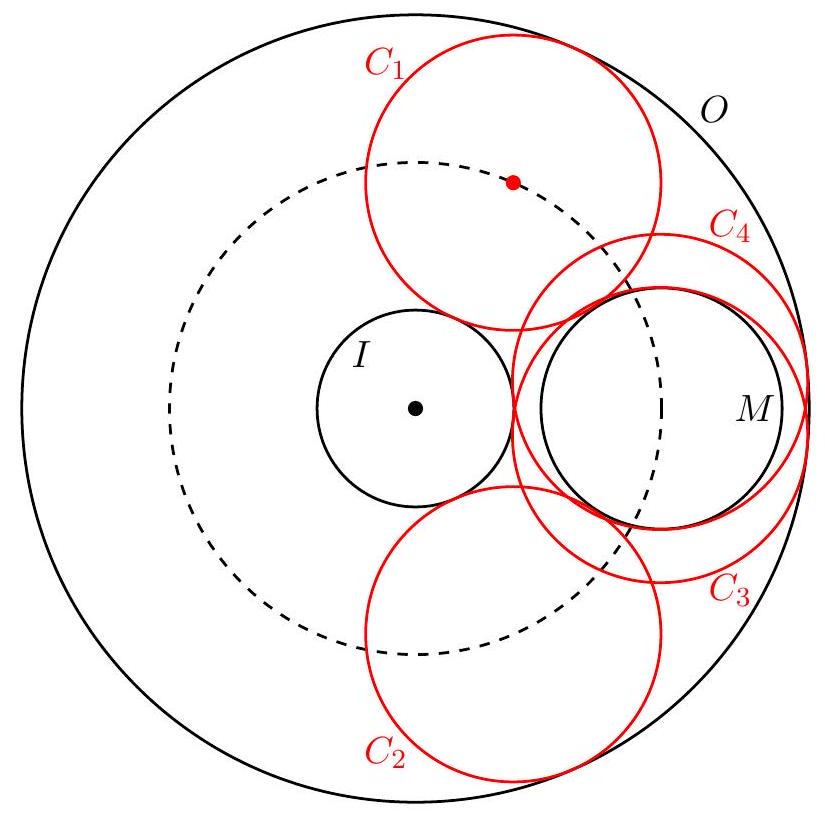
If circle is externally tangent to , then the diameter of is , so has radius 3 . Imagine rotating around the origin, with its center units from the origin. There are two positions in which circle is externally tangent to and two positions in which is internally tangent to . This gives four circles of radius 3 that meet the conditions of the problem, as shown below.
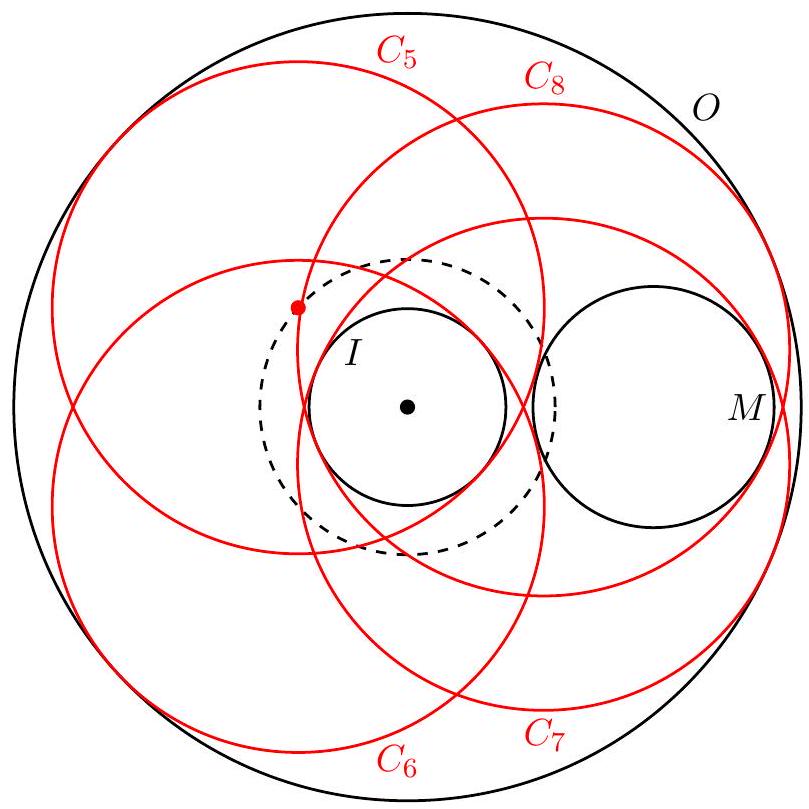
If circle is internally tangent to , then the diameter of is , so has radius 5 . Imagine rotating around the origin, with its center units from the origin. There are two positions in which circle is externally tangent to and two positions in which is internally tangent to . This gives four circles of radius 5 that meet the conditions of the problem, as shown below.
The total area of these eight circles is .
Note: Problems like this one were studied by the ancient Greek mathematician and astronomer Apollonius of Perga.
The problems on this page are the property of the MAA's American Mathematics Competitions