Problem:
The figure below is a map showing 12 cities and 17 roads connecting certain pairs of cities. Paula wishes to travel along exactly 13 of those roads, starting at city and ending at city , without traveling along any portion of a road more than once. (Paula is allowed to visit a city more than once.) How many different routes can Paula take?
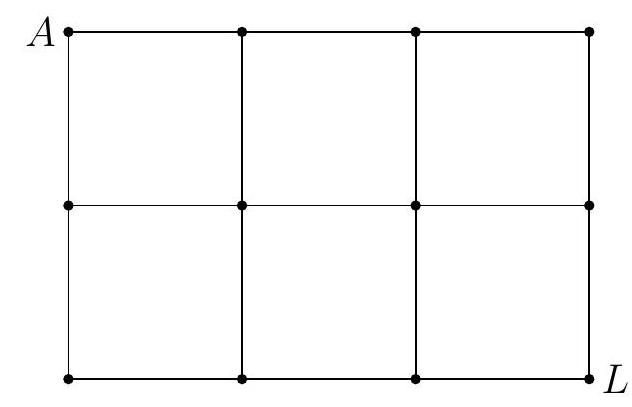
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Note that of the cities, of them ( on the top, on the bottom, and on each side) have edges coming into/out of them (i.e., in graph theory terms, they have degree ). Therefore, at least edge connecting to each of these cities cannot be used. Additionally, the same applies to the start and end points, since we don't want to return to them. Thus there are vertices that we know have unused edge, and we have unused edges to work with (since there are edges in total, and we must use exactly of them). It is not hard to find that there is only one configuration satisfying these conditions:
Note: Xs represent unused edges.
.jpg)
Observe that at each of the cities marked with an on a path, there are possibilities: we can either continue straight and cross back over the path later, or we can make a left turn, then turn right when we approach the junction again. This gives us a total of valid paths.
The problems on this page are the property of the MAA's American Mathematics Competitions