Problem:
The figure below shows a dotted grid 8 cells wide and 3 cells tall consisting of squares. Carl places 1 -inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
There are two possibilities for the loop if it does not cross the middle row of an rectangle around the top row of cells or an rectangle around the bottom row of cells. Otherwise, wherever the loop crosses the middle row, it must proceed straight in both directions after the middle row. This divides the dotted grid into two connected components, and both ends of the loop must enter the same connected component. It follows that the loop must cross one of the leftmost two columns and one of the rightmost two columns for a total of four configurations.
.jpg)
In each case there are two ends of the loop that must connect-one across the top and one across the bottom-along with some number of 1 s in the middle of the grid. Suppose there are such 1 s . For each 1 , the loop can cover either the top edge or the bottom edge. These choices are independent of each other, so the number of ways to connect both ends of the loop is . The figure below demonstrates one possibility when .
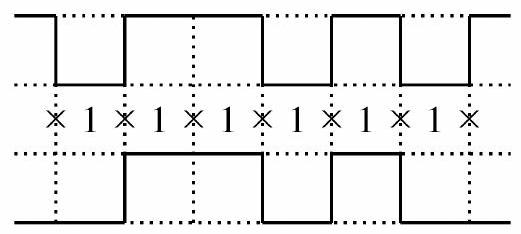
Of the four possibilities for what happens at the ends, one gives , two give , and one gives . The total number of solutions is
Note: The rules for laying matchsticks mirror those found in the logic puzzle genre Slitherlink, which originated from Japan in the early 1990s.
The problems on this page are the property of the MAA's American Mathematics Competitions