Problem:
Let f(x)=∣2{x}−1∣ where {x} denotes the fractional part of x. The number n is the smallest positive integer such that the equation
nf(xf(x))=x
has at least 2012 real solutions x. What is n ?
Note: the fractional part of x is a real number y={x}, such that 0≤y<1 and x−y is an integer.
Answer Choices:
A. 30
B. 31
C. 32
D. 62
E. 64
Solution:
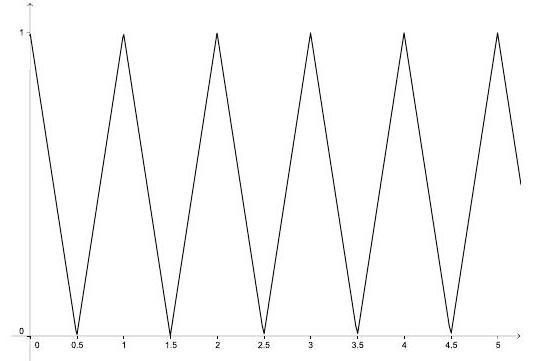
Because −1≤2{x}−1≤1 it follows that 0≤f(x)≤1 for all x∈R. Thus 0≤nf(xf(x))≤n, and therefore all real solutions x of the required equation are in the interval [0,n]. Also f(x) is periodic with period 1 , f(x)=1−2x if 0≤x≤21, and f(x)=2x−1 if 21≤x≤1. Thus the graph of y=f(x) for x≥0 consists of line segments joining the points with coordinates (k,1),(k+21,0),(k+1,1) for integers k≥0 as shown.
Let a be an integer such that 0≤a≤n−1. Consider the interval [a,a+21). If x∈[a,a+21), then f(x)=∣2{x}−1∣=∣2(x−a)−1∣=1+2a−2x and thus g(x):=xf(x)=x(1+2a−2x). Suppose a≥1 and a≤x<y<a+21. Then 2x+2y−2a−1>2a−1≥1 and so (y−x)(2x+2y−2a−1)>0, which is equivalent to g(x)=x(1+2a−2x)>y(1+2a−2y)=g(y). Thus g is strictly decreasing on [a,a+21) and so it maps [a,a+21) bijectively to (0,a]. Thus the graph of the function y=f(g(x)) on the interval [a,a+21) oscillates from 1 to 0 as many times as the graph of the function y=f(x) on the interval (0,a]. It follows that the line with equation y=nx intersects the graph of y=f(g(x)) on the interval [a,a+21) exactly 2a times.
If a=0 and x∈[a,a+21), then g(x)=x(1−2x) satisfies 0≤g(x)≤81, so f(g(x))=1−2g(x)=4x2−2x+1. If x∈[0,21) and n≥1, then 0≤nx<2n1≤21. Because 21≤1−2g(x)≤1, it follows that the parabola y=f(g(x)) does not intersect any of the lines with equation y=nx on the interval [0,21).
Similarly, if x∈[a+21,a+1), then f(x)=∣2{x}−1∣=∣2(x−a)−1∣=2x−2a−1 and g(x):=xf(x)=x(2x−2a−1). This time if a+21≤x<y<a+1, then 2x+2y−2a+1≥2a+1≥1 and so (x−y)(2x+2y−2a+1)<0, which is equivalent to g(x)<g(y). Thus g is strictly increasing on [a+21,a+1) and so it maps [a+21,a+1) bijectively to [0,a+1). Thus the graph of the function y=f(g(x)) on the interval [a+21,a+1) oscillates as many times as the graph of y=f(x) on the interval [0,a+1). It follows that the line with equation y=nx intersects the graph of y=f(g(x)) on the interval [a+21,a+1) exactly 2(a+1)
times. Therefore the total number of intersections of the line y=nx and the graph of y=f(g(x)) is equal to
a=0∑n−1(2a+2(a+1))=2a=0∑n−1(2a+1)=2n2
Finally the smallest n such that 2n2≥2012 is n=32 because 2⋅312=1922 and 2⋅322=2048.
The problems on this page are the property of the MAA's American Mathematics Competitions