Problem:
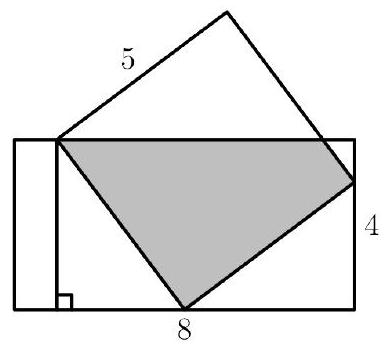
The diagram below shows a rectangle with side lengths and and a square with side length . Three vertices of the square lie on three different sides of the rectangle, as shown. What is the area of the region inside both the square and the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Label the square counterclockwise , where is the vertex outside the rectangle, and let be the intersection of with the top side of the rectangle. Let be the projection of onto the side of the rectangle containing , as shown.
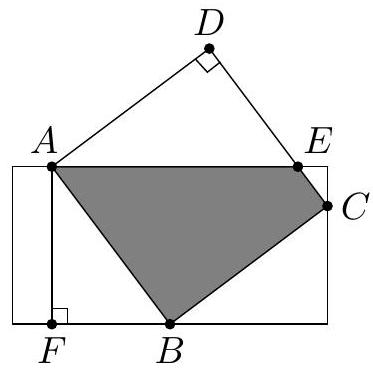
Then the side lengths of are , and by the Pythagorean Theorem . By alternate interior angles, , so . Therefore . It follows that the area of is . The requested area of the region inside both the square and the rectangle is the area of the square minus the area of , which is .
The problems on this page are the property of the MAA's American Mathematics Competitions