Problem:
A disphenoid is a tetrahedron whose triangular faces are congruent to one another. What is the least total surface area of a disphenoid whose faces are scalene triangles with integer side lengths?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
First note that adjacent faces must be rotations of one another to create a disphenoid (see the figure below). If they were instead mirrored, then the other two faces would be isosceles (and be neither scalene nor congruent to the others, as required).
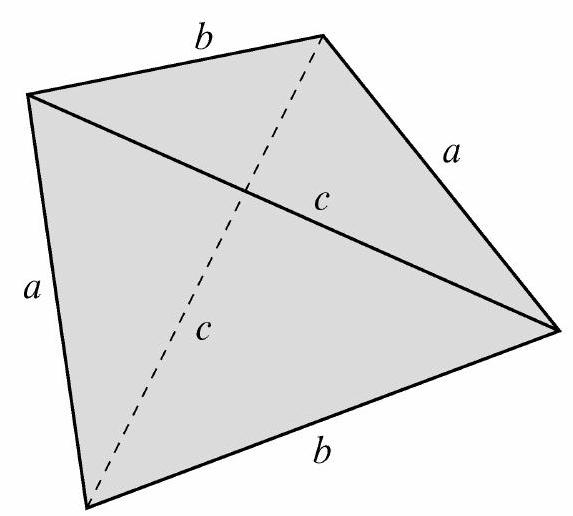
Next, to determine what triangles could form a disphenoid, let the positive integer side lengths be , , and , with . Consider two faces of the tetrahedron that have their sides of length in common. That common edge can be thought of as a "hinge" between two faces. If those two faces were laid flat, they would form a parallelogram with one diagonal of length . When folded over the hinge, the other diagonal of the parallelogram becomes two sides of a triangle whose third side is the last edge of the tetrahedron. (Note that this last edge must have length to create the disphenoid.) If the sides of length and formed a right angle, then the parallelogram would be a rectangle, and the other diagonal would also have length . A tetrahedron formed by folding the triangles over the hinge would have its last edge shorter than , making it not a disphenoid. If instead the sides of length and formed an obtuse angle, the other diagonal would be shorter than , and folding would make the last edge shorter yet (and again not a disphenoid). Thus the faces must be acute to form a disphenoid.
To minimize the surface area, , and must be the least distinct integers that form an acute triangle. Note that 2, 3, and 4 form an obtuse triangle (because ); and 3, 4, and 5 form a right triangle. However, , so 4,5 , and 6 form an acute triangle with the least area. The area of one face can be computed using Heron's Formula. The triangle's semiperimeter is , and the disphenoid's total surface area is
Another way to find the area of a face is to use the formula . By the Law of Cosines,
Then
Therefore the area of one face is
and the total surface area is .
The problems on this page are the property of the MAA's American Mathematics Competitions