Problem:
A lampshade is made in the form of the lateral surface of the frustum of a right circular cone. The height of the frustum is inches, its top diameter is inches, and its bottom diameter is inches. A bug is at the bottom of the lampshade and there is a glob of honey on the top edge of the lampshade at the spot farthest from the bug. The bug wants to crawl to the honey, but it must stay on the surface of the lampshade. What is the length in inches of its shortest path to the honey?
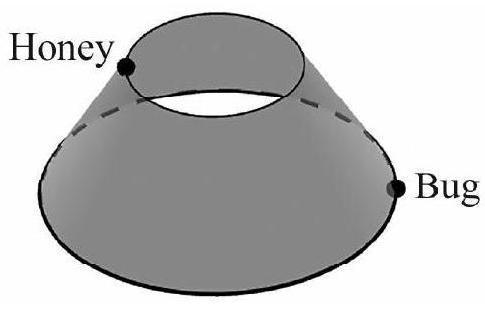
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The circumference of the bottom of the cone is , the height of the (full) cone is , and the slant height of the cone is 12 .
.jpg)
When the frustum is slit along the slant height and rolled out (into a sector of an annulus), the outer radius will be 12 and the arc length will be , making the measure of the arc .
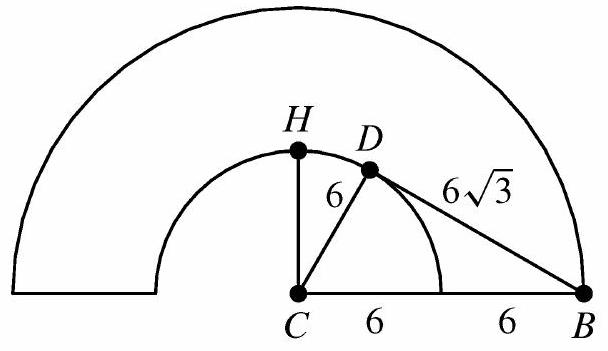
Refer to the unrolled figure. The bug wants to crawl from point to point . Note that because is at the top of the inner semicircle and is to the right of its center, passes through the interior of the semicircle and thus does not remain on the surface of the lampshade, as required. Therefore the bug will need to crawl from to (where is tangent to the inner circle), then along the\
semicircle to . The inside radius is 6 , so is a right triangle and . Because and , it follows that . Therefore the length of is
The length of the path from to to is inches.
The problems on this page are the property of the MAA's American Mathematics Competitions