Problem:
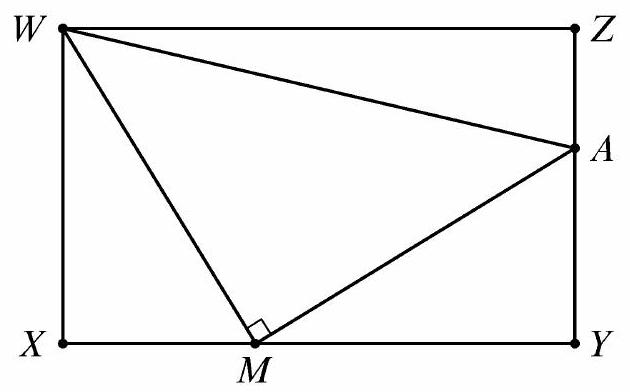
In the figure below WXYZ is a rectangle with WX=4 and WZ=8. Point M lies on XY, point A lies on YZ, and ∠WMA is a right angle. The areas of triangles △WXM and △WAZ are equal. What is the area of △WMA ?
Answer Choices:
A. 13
B. 14
C. 15
D. 16
E. 17
Solution:
Label the diagram as shown, where MX=a and ZA=b.
The Pythagorean Theorem on △WMA gives WM2+MA2=WA2, which implies that
42+a2+(8−a)2+(4−b)2=82+b2
Expanding and simplifying yields a2−8a−4b+16=0. Because the areas of triangles △WXM and △WAZ are equal, 21⋅4a=21⋅8b, so a=2b. Substituting into the previous equation and factoring gives 4(b−1)(b−4)=0. Therefore b=1 or b=4. But b=4 would require A=Y=M, and ∠WMA would not exist, so it must be that b=1 and a=2. The area of △WMA can be found by subtracting the three other triangle areas from the area of the rectangle:
8⋅4−21⋅4⋅2−21⋅6⋅3−21⋅8⋅1=32−4−9−4=(C)15
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)