Problem:
A closed box with a square base is to be wrapped with a square sheet of wrapping paper. The box is centered on the wrapping paper with the vertices of the base lying on the midlines of the square sheet of paper, as shown in the figure on the left. The four corners of the wrapping paper are to be folded up over the sides and brought together to meet at the center of the top of the box, point in the figure on the right. The box has base length and height . What is the area of the sheet of wrapping paper?
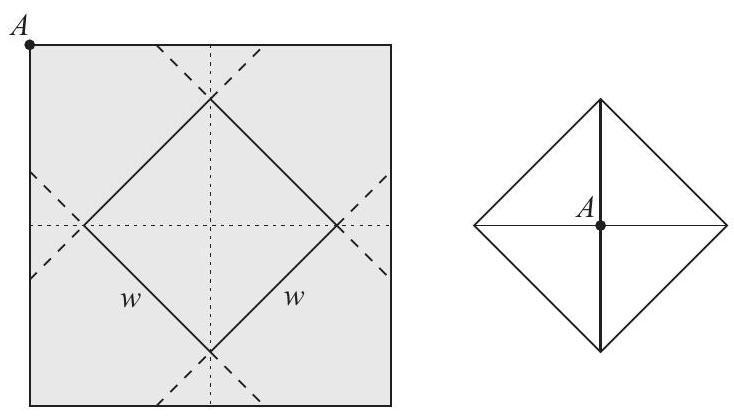
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The figure shows that the distance from a corner of the wrapping paper to the center is
The side of the wrapping paper, in the figure, is the hypotenuse of a right triangle, so its length is . Therefore the area of the wrapping paper is
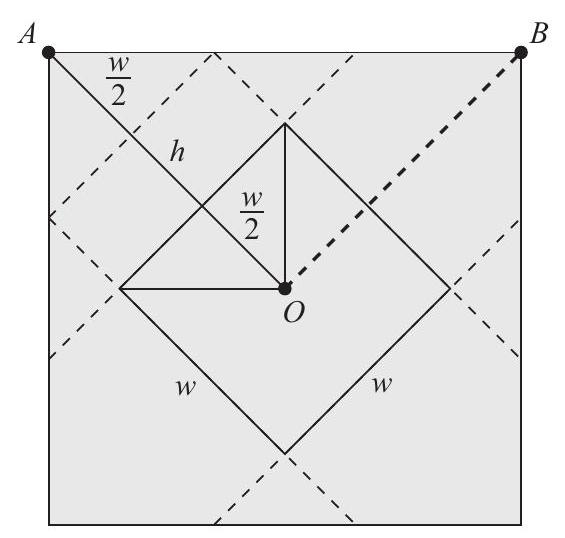
OR
The area of the wrapping paper, excluding the four small triangles indicated by the dashed lines, is equal to the surface area of the box, which is . The four triangles are isosceles right triangles with leg length , so their combined area is . Thus the total area of the wrapping paper is .
The problems on this page are the property of the MAA's American Mathematics Competitions