Problem:
When the roots of the polynomial
are removed from the real number line, what remains is the union of disjoint open intervals. On how many of these intervals is positive?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Note that the function for . Moving right to left along the real number line, changes sign precisely when passing through a root of odd multiplicity. This means that the function changes sign as passes through , and 1 , and its value is 0 at , and 2 as well. Therefore on the intervals , and , a total of intervals.
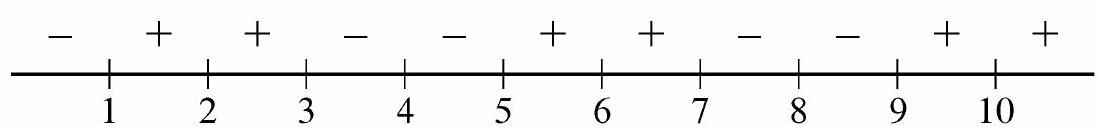
Perfect square factors are always nonnegative, so they can be removed without changing the signs. Therefore, for any with , the polynomial
will have the same sign as . Now is positive on the following intervals: and (where four of the factors are negative), and (where two of the factors are negative), and and (where all the factors are positive). This gives a total of intervals on which . On the other 5 intervals there are an odd number of negative factors, so , and therefore as well, is negative.
The problems on this page are the property of the MAA's American Mathematics Competitions