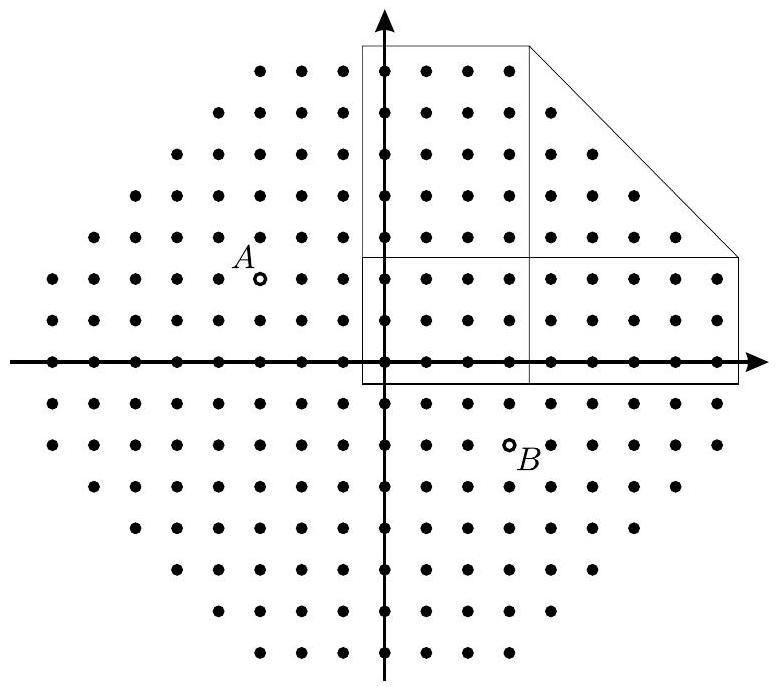
Problem:
A bug travels in the coordinate plane, moving only along the lines that are parallel to the x-axis or y-axis. Let A=(−3,2) and B=(3,−2). Consider all possible paths of the bug from A to B of length at most 20. How many points with integer coordinates lie on at least one of these paths?
Answer Choices:
A. 161
B. 185
C. 195
D. 227
E. 255
Solution:
Let X=(x,y). The distance traveled by the bug from A to X is at least ∣x+3∣+∣y−2∣. Similarly, the distance traveled by the bug from X to B is at least ∣x−3∣+∣y+2∣. It follows that X belongs to a path from A to B traveled by the bug if and only if
d=∣x−3∣+∣x+3∣+∣y−2∣+∣y+2∣≤20
The expression for d is invariant if x is replaced by −x or y is replaced by −y. By symmetry, it is enough to count the number of points X with x≥0 and y≥0, multiply by 4 , and subtract the points that were overcounted, that is those in the x-axis or in the y-axis. Consider four cases:
Case 1. 0≤x≤3 and 0≤y≤2. In this case ∣x−3∣+∣x+3∣=6 and ∣y−2∣+∣y+2∣=4. Thus d=10<20 and there are 4⋅3=12 points X in this case. This includes the origin and 5 other points for which xy=0.
Case 2. 0≤x≤3 and y≥3. In this case ∣x−3∣+∣x+3∣=6 and ∣y−2∣+∣y+2∣= 2y. Thus d=6+2y≤20 if and only if y≤7. There are 4⋅5=20 points X in this case. This includes 5 points for which xy=0.
Case 3. x≥4 and 0≤y≤2. In this case ∣x−3∣+∣x+3∣=2x and ∣y−2∣+∣y+2∣=4. Thus d=4+2x≤20 if and only if x≤8. There are 5⋅3=15 points X in this case. This includes 5 points for which xy=0.
Case 4. x≥4 and y≥3. In this case ∣x−3∣+∣x+3∣=2x and ∣y−2∣+∣y+2∣=2y. Thus d=2x+2y≤20 if and only if x+y≤10. The number of points X in this case is equal to
x=4∑7y=3∑10−x1=x=4∑7(10−x−2)=x=4∑7(8−x)=4+3+2+1=10
and there are no points with xy=0.
By symmetry the required total is 4(12+20+15+10)−2(5+5+5)−3= 4⋅57−2⋅15−3=195.
The problems on this page are the property of the MAA's American Mathematics Competitions