Problem:
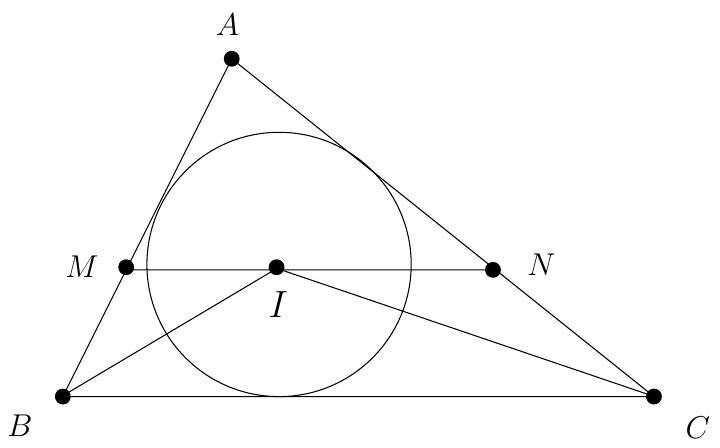
Triangle ABC has side-lengths AB=12,BC=24, and AC=18. The line through the incenter of △ABC parallel to BC intersects AB at M and AC at N. What is the perimeter of △AMN ?
Answer Choices:
A. 27
B. 30
C. 33
D. 36
E. 42
Solution:
Let I be the incenter of △ABC. Because I is the intersection of the angle bisectors of the triangle and MN is parallel to BC, it follows that ∠IBM=∠CBI=∠MIB and ∠NCI=∠ICB=∠CIN. Hence △BMI and\
△CNI are isosceles with MB=MI and CN=IN. Thus the perimeter of △AMN is
AM+MN+NA=AM+MI+IN+NA=AM+MB+CN+NA=AB+AC=12+18=30
The problems on this page are the property of the MAA's American Mathematics Competitions