Problem:
Consider the set of 30 parabolas defined as follows: all parabolas have as focus the point and the directrix lines have the form with and integers such that and . No three of these parabolas have a common point. How many points in the plane are on two of these parabolas?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
If the directrices of two parabolas with the same focus intersect, then the corresponding parabolas intersect in exactly two points. The same conclusion holds if the directrices are parallel and the focus is between the two lines. Moreover, if the directrices are parallel and the focus is not between the two lines, then the corresponding parabolas do not intersect. Indeed, a point belongs to the intersection of the parabolas with focus and directrices and , if and only if, . That is, the circle with center and radius is tangent to both and . If and are parallel and is not between them, then clearly such circle does not exist. If and intersect and is not on them, then there are are exactly two circles tangent to both and that go through . The same is true if and are parallel and is between them.
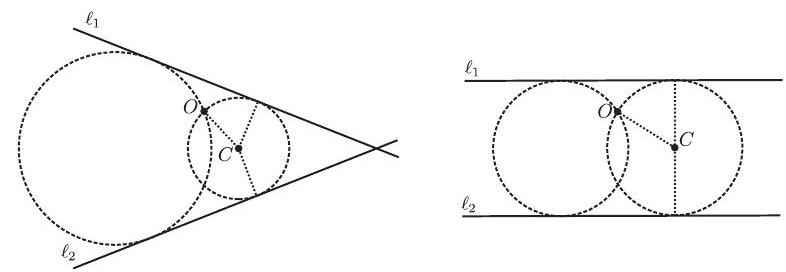
Thus there are pairs of parabolas and the pairs that do not intersect are exactly those whose directrices have the same slope and whose -intercepts have the same sign. There are 5 different slopes and pairs of -intercepts with the same sign taken from . Because the pairs of parabolas that intersect do so at exactly two points and no point is in three parabolas, it follows that the total number of intersection points is
Note: It is possible to construct the two circles through and tangent to the lines and as follows: Let be the bisector of the angle determined by the angular sector spanned by and that contains (or the midline of and if these lines are parallel and is between them). Let be the symmetric point of with respect to and let be the intersection of and the line (if then let be the intersection of and a perpendicular line to by ). If is one of the desired circles, then passes through and and is tangent to . Let be the point of tangency of and . By the Power of a Point Theorem, . The circle with center and radius intersects in two points and . The circumcircles of and are the desired circles.
.jpg)
The problems on this page are the property of the MAA's American Mathematics Competitions