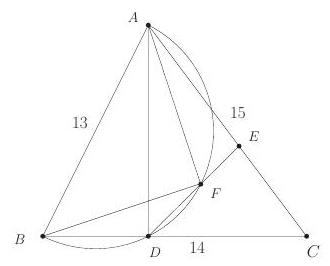
Problem:
In triangle ABC,AB=13,BC=14, and CA=15. Distinct points D,E, and F lie on segments BC,CA, and DE, respectively, such that AD⊥BC, DE⊥AC, and AF⊥BF. The length of segment DF can be written as nm, where m and n are relatively prime positive integers. What is m+n ?
Answer Choices:
A. 18
B. 21
C. 24
D. 27
E. 30
Solution:
The Pythagorean Theorem applied to right triangles ABD and ACD gives AB2−BD2=AD2=AC2−CD2; that is, 132−BD2= 152−(14−BD)2, from which it follows that BD=5,CD=9, and AD=12. Because triangles AED and ADC are similar,
12AE=9DE=1512
implying that ED=536 and AE=548.
Because ∠AFB=∠ADB=90∘, it follows that ABDF is cyclic. Thus ∠ABD+ ∠AFD=180∘ from which ∠ABD=∠AFE. Therefore right triangles ABD and AFE are similar. Hence
5FE=12548
from which it follows that FE=4. Consequently DF=DE−FE=536−4= 516.
The problems on this page are the property of the MAA's American Mathematics Competitions