Problem:
Square ABCD has side length 30 . Point P lies inside the square so that AP=12 and BP=26. The centroids of â–³ABP,â–³BCP, â–³CDP, and â–³DAP are the vertices of a convex quadrilateral. What is the area of that quadrilateral?
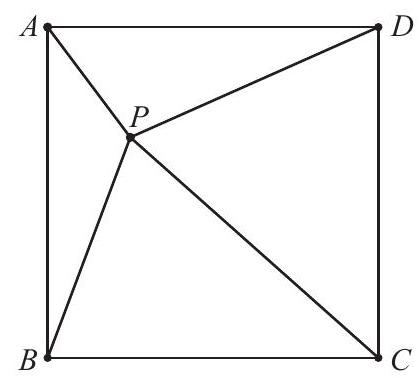
Answer Choices:
A. 1002​
B. 1003​
C. 200
D. 2002​
E. 2003​ Solution:
Let E and F be the midpoints of sides BC and CD, respectively. Let G and H be the centroids of △BCP and △CDP, respectively. Then G is on PE, a median of △BCP, a distance 32​ of the way from P to E. Similarly, H is on PF a distance 32​ of the way from P to F. Thus GH is parallel to EF and 32​ the length of EF. Because BC=30, it follows that EC=15,EF=152​, and GH=102​. The midpoints of AB,BC,CD, and DA form a square, so the centroids of △ABP,△BCP,△CDP, and △DAP also form a square, and that square has side length 102​. The requested area is (102​)2=200​.
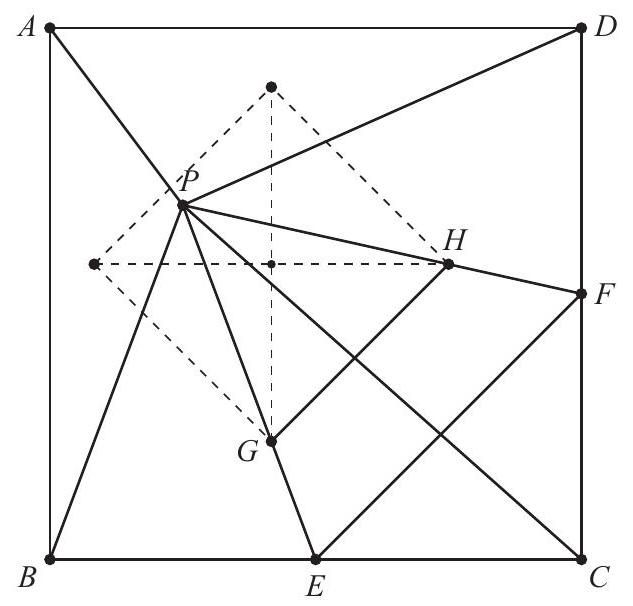
OR
Place the figure in the coordinate plane with A=(0,30),B=(0,0), C=(30,0),D=(30,30), and P=(3x,3y). Then the coordinates of the centroids of the four triangles are found by averaging the coordinates of the vertices: (x,y+10),(x+10,y),(x+20,y+10), and (x+10,y+20). It can be seen that the quadrilateral formed by the centroids is a square with center (x+10,y+10) and vertices aligned vertically and horizontally. Its area is half the product of the lengths of its diagonals, 21​⋅20⋅20=200​.
Note: As the solutions demonstrate, the inner quadrilateral is always a square, and its size is independent of the location of point P. The location of the square within square ABCD does depend on the location of P.
