Problem:
On top of a rectangular card with sides of length 1 and , an identical card is placed so that two of their diagonals line up, as shown ( , in this case).
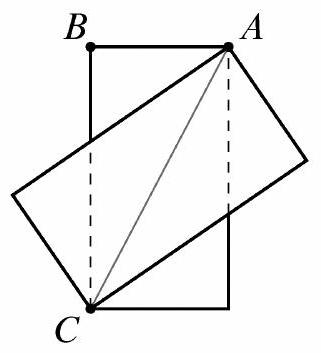
Continue the process, adding a third card to the second, and so on, lining up successive diagonals after rotating clockwise. In total, how many cards must be used until a vertex of a new card lands exactly on the vertex labeled in the figure?
Answer Choices:
A.
B.
C.
D.
E. No new vertex will land on
Solution:
Note that the common diagonal is a diameter of the circle that will ultimately circumscribe the collection of rectangles. Each rectangle is composed of four chords of the circle, and the set of outermost chords will form a regular -gon if a vertex lands on . Because each new card contributes two sides of the polygon, the problem is asking for . Let be the center of the circle.
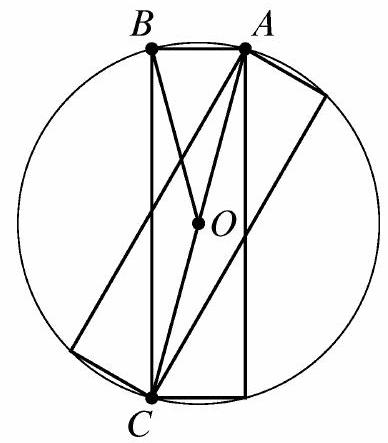
Let . Then the measure of minor arc \wideparen{A B} is , and . Because and ,
Each card is rotated through an angle compared to the previous card. A Double Angle Formula gives
This value is recognizable as , so and . The polygon is a dodecagon. It will take just cards to complete the dodecagon and have a new vertex land on vertex , as illustrated below.
.jpg)
The problems on this page are the property of the MAA's American Mathematics Competitions