Problem:
The internal angles of quadrilateral form an arithmetic progression. Triangles and are similar with and . Moreover, the angles in each of these two triangles also form an arithmetic progression. In degrees, what is the largest possible sum of the two largest angles of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the degree measures of the angles be as shown in the figure. The angles of a triangle form an arithmetic progression if and only if the median angle is , so one of , or must be equal to 60 . By symmetry of the role of the triangles and , assume that . Because and , it follows that the arithmetic progression of the angles in from smallest to largest must be either or . Thus either , in which case ; or , in which case . Neither of these is compatible with (the former forces and the latter forces ), so either or .
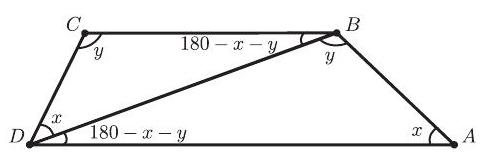
First suppose that . If , then , and the sequence of angles in is . If , then , and the sequence of angles in is . Finally, suppose that . If , then , and the sequence of angles in is . If , then and , which is impossible.
Therefore, the sum in degrees of the two largest possible angles is .
The problems on this page are the property of the MAA's American Mathematics Competitions