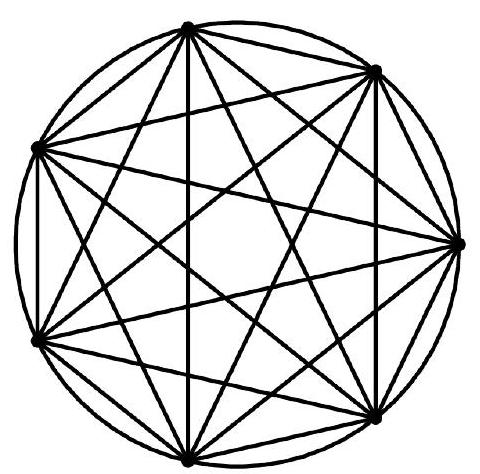
Problem:
The figure below depicts a regular 7-gon inscribed in a unit circle.
What is the sum of the 4 th powers of the lengths of all 21 of its edges and diagonals?
Answer Choices:
A. 49
B. 98
C. 147
D. 168
E. 196
Solution:
Recall that if v and w are arbitrary complex numbers, then the following identities hold:
∣w∣2=wwˉ,v+w=vˉ+wˉ, and vw=vˉwˉ,
where wˉ denotes the complex conjugate of w. Hence if z is a complex number, then
∣z−1∣2=(z−1)(z−1)=(z−1)(zˉ−1)=zzˉ−z−zˉ+1=∣z∣2−z−zˉ+1
From now on, assume that ∣z∣=1. For such z, the above gives ∣z−1∣2=2−z−zˉ. Hence
∣z−1∣4=(2−z−zˉ)2.
Expanding and collecting like terms yield
∣z−1∣4=z2−4z+6−4zˉ+zˉ2.
Now set
z=cis(72π)=cos72π+isin72π=e72πi
Thus 1,z,z2,z3,z4,z5,z6 are the vertices of a regular 7 -gon inscribed in the unit circle in the complex plane, zˉ=z−1, and z7=1. The sum of the 4th powers of the lengths of the edges and diagonals with one endpoint at 1 is therefore
S=k=1∑6∣∣∣zk−1∣∣∣4.
If k=0 were allowed in this sum, then the contribution would be ∣∣∣z0−1∣∣∣4=∣1−1∣4=0. Thus
S=k=0∑6∣∣∣zk−1∣∣∣4=k=0∑6(z2k−4zk+6−4z−k+z−2k)
=T(2)−4T(1)+6T(0)−4T(−1)+T(−2)
where
T(a)=k=0∑6zak
Suppose that a is an integer, and that 7 does not divide a. Then za=1, so by the formula for the sum of a geometric progression,
T(a)=1−za1−z7a=1−za1−1=0
Thus S=6T(0)=6⋅7. The other vertices make the same contribution, which gives a total of 6⋅72. However, each edge and each diagonal has two endpoints, so all contributions have been counted twice. Hence the requested total is 3⋅72=(C)147.
The problems on this page are the property of the MAA's American Mathematics Competitions