Problem:
A circle having center , with , is tangent to the lines and . What is the radius of this circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
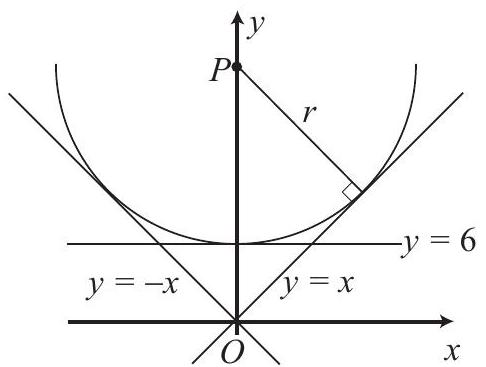
Let denote the origin, the center of the circle, and the radius. A radius from the center to the point of tangency with the line forms a right triangle with hypotenuse . This right triangle is isosceles since the line forms a angle with the -axis. So
{OR}
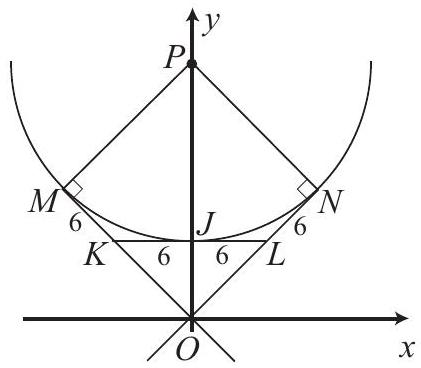
Let the line intersect the circle and the line at and , respectively, and let the line intersect the circle and the line at and , respectively. Quadrilateral has four right angles and , so is a square. In addition, and . Hence
The problems on this page are the property of the MAA's American Mathematics Competitions