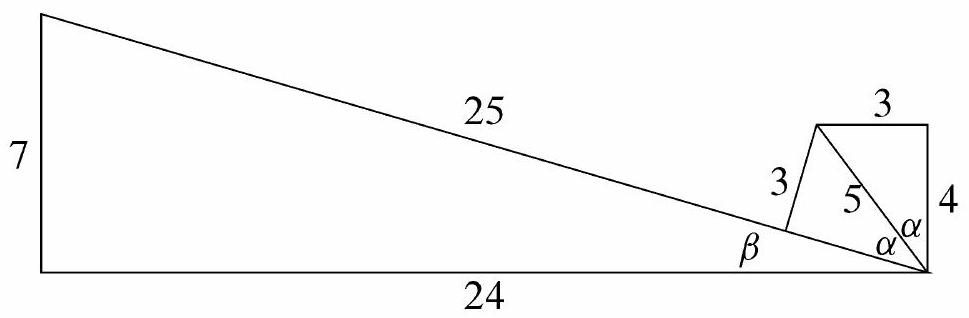
Problem:
Let α be the radian measure of the smallest angle in a 3−4−5 right triangle. Let β be the radian measure of the smallest angle in a 7-24-25 right triangle. In terms of α, what is β ?
Answer Choices:
A. 3α
B. α−8π
C. 2π−2α
D. 2α
E. π−4α
Solution:
Because α and β are the smallest angles in these triangles, sinα=53,cosα=54, sinβ=257, and cosβ=2524. By a Double Angle Formula,
sin(2α)=2sinα⋅cosα=2⋅53⋅54=2524=cosβ=sin(2π−β)
Because both 2α and β are acute, 2α=2π−β, so β=(C)2π−2α.
OR
Using complex numbers in polar form, 4+3i=5(cosα+isinα). Squaring gives 7+24i= 25(cosα+isinα)2. Similarly, 24+7i=25(cosβ+isinβ). Multiplying these two equations yields
(7+24i)(24+7i)625icos2π+isin2π=25(cosα+isinα)2⋅25(cosβ+isinβ)=625(cos(2α+β)+isin(2α+β))=cos(2α+β)+isin(2α+β).
Because both 2α and β are acute, 2α+β=2π and β=(C)2π−2α.
Note: The angles are α≈36.87∘ and β≈16.26∘.
The problems on this page are the property of the MAA's American Mathematics Competitions