Problem:
Suppose is a complex number with positive imaginary part, with real part greater than 1 , and with . In the complex plane, the four values , and are the vertices of a quadrilateral with area 15 . What is the imaginary part of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the argument of . Because and the real part of is greater than 1 , it follows that is less than . This ensures that the imaginary parts of and are positive and all the vertices of the quadrilateral other than 0 lie in the upper half-plane. Thus the area of the quadrilateral is the sum of the areas of the triangle with vertices , and and the triangle with vertices , and . See the figure.
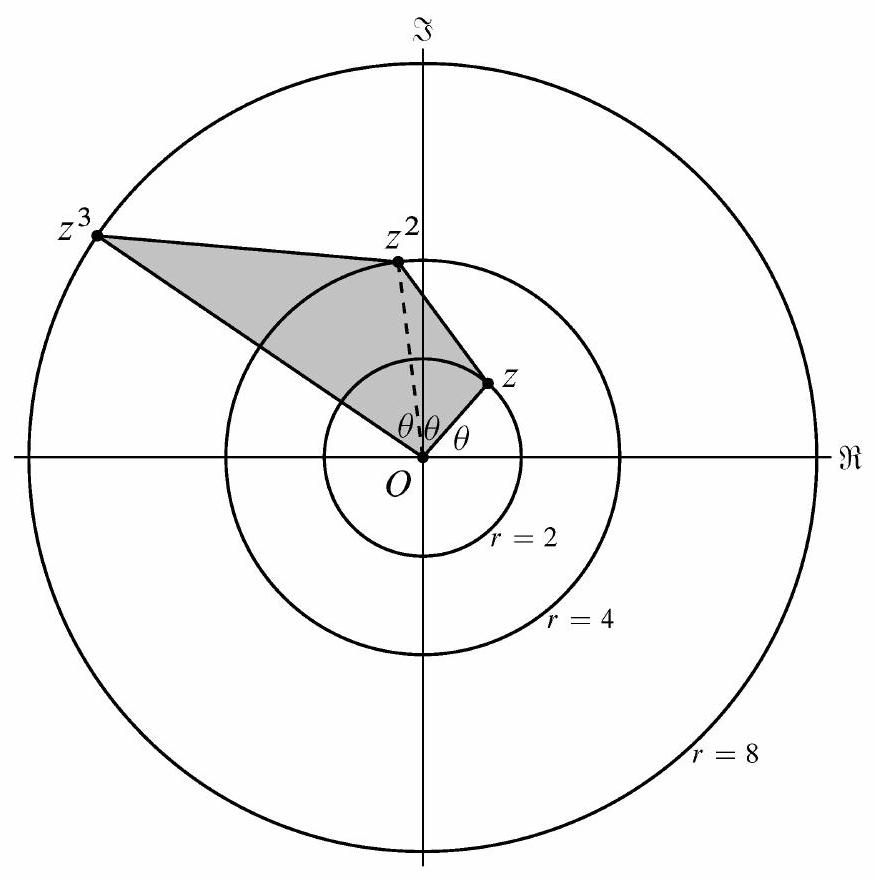
Because the area of a triangle with side lengths and with included angle is , the area of the quadrilateral must be
It follows that , and the imaginary part of is .
The problems on this page are the property of the MAA's American Mathematics Competitions