Problem:
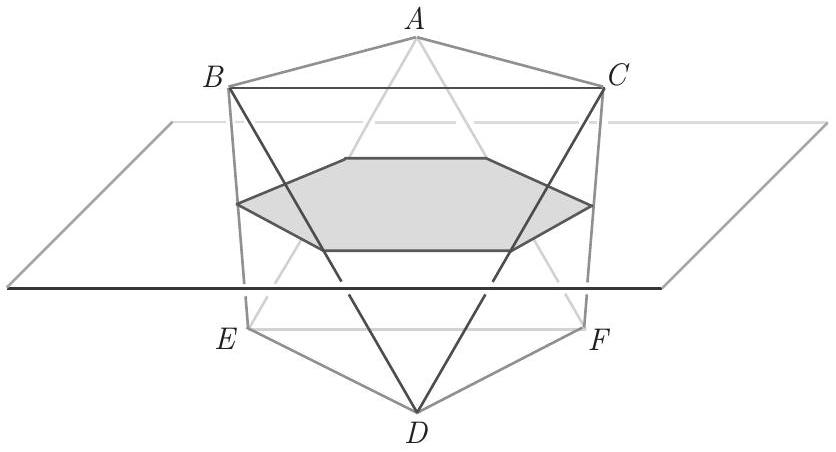
A regular octahedron has side length 1. A plane parallel to two of its opposite faces cuts the octahedron into two congruent solids. The polygon formed by the intersection of the plane and the octahedron has area , where , and are positive integers, and are relatively prime, and is not divisible by the square of any prime. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let and be the two faces of the octahedron parallel to the cutting plane. The plane passes through the midpoints of the six edges of the octahedron that are not sides of either of those triangles. Hence the intersection of the plane with the octahedron is an equilateral hexagon with side length . Then by symmetry the hexagon is also equiangular and hence regular. The area of the hexagon is 6 times that of an equilateral triangle with side length , so the area is . Therefore .
The problems on this page are the property of the MAA's American Mathematics Competitions