Problem:
Let and be circles defined by
and
respectively. What is the length of the shortest line segment that is tangent to at and to at ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
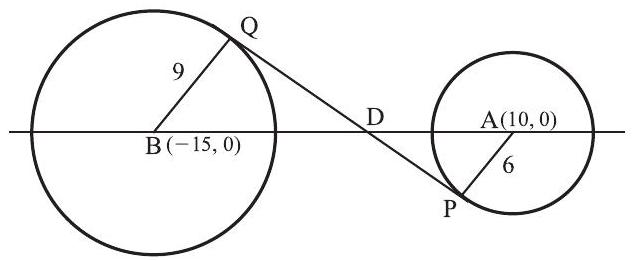
The centers are at and , and the radii are 6 and 9 , respectively. Since the internal tangent is shorter than the external tangent, intersects at a point that divides into parts proportional to the radii. The right triangles and are similar with ratio of similarity . Therefore, , and . Thus .
The problems on this page are the property of the MAA's American Mathematics Competitions