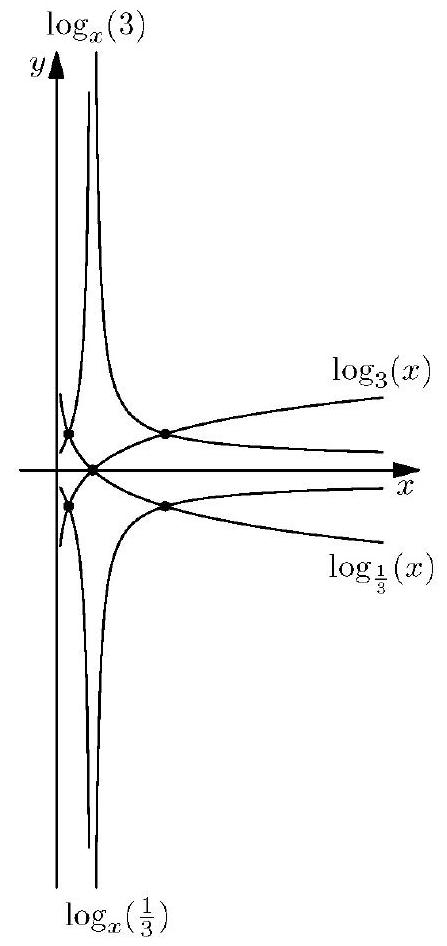
Problem:
The graphs of y=log3x,y=logx3,y=log31x, and y=logx31 are plotted on the same set of axes. How many points in the plane with positive x-coordinates lie on two or more of the graphs?
Answer Choices:
A. 2
B. 3
C. 4
D. 5
E. 6
Solution:
Let u=log3x. Then logx3=u1,log31x=−u, and logx31=−u1. Thus each point at which two of the graphs of the given functions intersect in the (x,y)-plane corresponds to a point at which two of the graphs of y=u,y=u1, y=−u, and y=−u1 intersect in the (u,y)-plane. There are 5 such points (u,y), namely (0,0),(1,1),(−1,1),(1,−1), and (−1,−1). The corresponding points of intersection on the graphs of the given functions are (1,0),(3,1),(31,1),(3,−1), and (31,−1).
The problems on this page are the property of the MAA's American Mathematics Competitions