Problem:
A circle of radius passes through both foci of, and exactly four points on, the ellipse with equation . The set of all possible values of is an interval . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
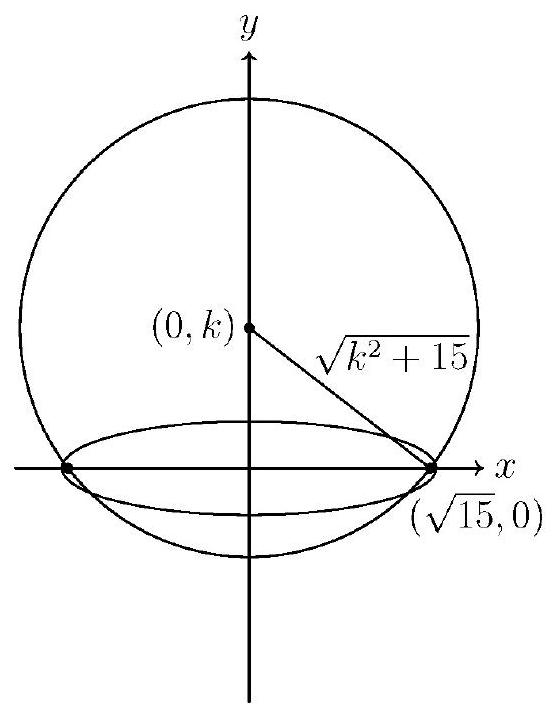
The ellipse with equation is centered at the origin, with a major axis of length 8 and a minor axis of length 2 . If the foci have coordinates , then . Thus . Any circle passing through both foci must have its center on the -axis; thus is at least as large as the distance from the foci to the -axis. That is, . For any , the circle of radius and center passes through both foci (in the interior of the ellipse) and the points . The point is in the exterior of the ellipse since 1. The point is in the exterior of the ellipse if and only if , that is, if and only if . Thus, for , the circle with center intersects the ellipse in four points if and only if . As increases, the radius increases as well, so the set of possible radii is the interval . The requested answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions