Problem:
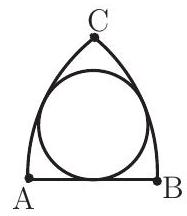
If circular arcs and have centers at and , respectively, then there exists a circle tangent to both and , and to . If the length of is , then the circumference of the circle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Construct the circle with center and radius . Let be the point of tangency of the two circles. Draw , and let be the point of intersection of and the given circle. By the Power of a Point Theorem, (see Note below). Let be the radius of the smaller circle. Since and are radii of the larger circle, and .
.jpg)
. Because , substitution into the first equation yields
or, equivalently, . Points , and are equidistant from each other, so \overparen{B C}=60^{\circ} and thus the circumference of the larger circle is length of \overparen{B C} ) . Let be the circumference of the smaller circle. Since the circumferences of the two circles are in the same ratio as their radii, . Therefore .
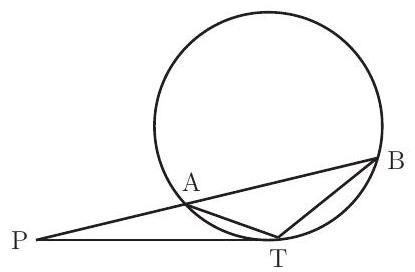
Note. From any exterior point , a secant and a tangent are drawn. Consider triangles and . They have a common angle . Since angles and intercept the same arc \overparen{A T}, they are congruent. Therefore triangles and are similar, and it follows that and . The number is called the power of the point with respect to the circle. Intersecting secants, tangents, and chords, paired in any manner create various cases of this theorem, which is sometimes called Crossed Chords.
The problems on this page are the property of the MAA's American Mathematics Competitions