Problem:
Rows , and of a triangular array of integers are shown below:
Each row after the first row is formed by placing a at each end of the row, and each interior entry is greater than the sum of the two numbers diagonally above it in the previous row. What is the units digit of the sum of the numbers in the rd row?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
The sums of the entries in the first 6 rows equal 1, 2, 5, 12, 27, and 58. Note that these sums equal for . That this formula is valid for arbitrary can be proved using mathematical induction, as follows. Let be the sum of the entries in row and assume the formula holds for row , i.e., . Each of the interior entries in row (other than the end 1s) contributes to , and the plus 1 rule for generating the array contributes another to . The end 1 s in row contribute 2 to , and the end 1 s of row add another 2 to . This gives
and the proof is complete. Thus the sum of the entries in the 2023rd row is .
It remains to compute the units digit of . Note that the units digits of successive powers of 2 form the sequence . Because 2023 leaves a remainder of 3 when divided by 4 , the units digit of is 8 . The requested units digit is therefore .
Let be the th entry in the th row of the array, and let . Then
for . Because satisfies this Pascal Identity together with the conditions , these values must be 2 times the binomial coefficients: . In other words, the resulting triangle is 2 times the ordinary Pascal Triangle.
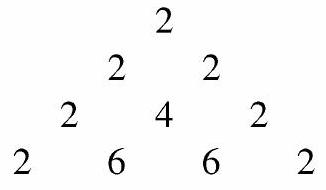
Therefore the sum of the 2023 entries in row 2023 of this array is , and the sum of the 2023 entries in row 2023 of the original array is , as above.
Note: The sequence whose th term is arises in many different contexts; see A000325 in the On-Line Encyclopedia of Integer Sequences.
The problems on this page are the property of the MAA's American Mathematics Competitions