Problem:
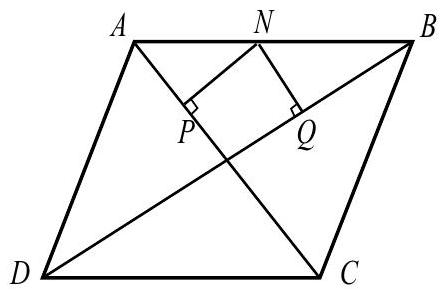
Let be a rhombus with and . Let be a point on , and let and be the feet of the perpendiculars from to and , respectively. Which of the following is closest to the minimum possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
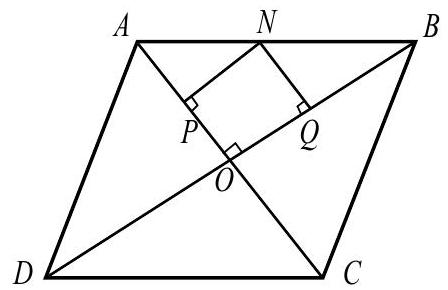
Let be the point of intersection of and . Then is a right triangle with legs and . Quadrilateral is a rectangle because it has right angles at , and . Thus , because the diagonals of a rectangle are of equal length. The minimum value of is the minimum value of . This is achieved if and only if is the foot of the altitude from in triangle . Writing the area of in two different ways yields
Hence the minimum value of is
The problems on this page are the property of the MAA's American Mathematics Competitions