Problem:
Michael walks at the rate of 5 feet per second on a long straight path. Trash pails are located every 200 feet along the path. A garbage truck travels at 10 feet per second in the same direction as Michael and stops for 30 seconds at each pail. As Michael passes a pail, he notices the truck ahead of him just leaving the next pail. How many times will Michael and the truck meet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Number the pails consecutively so that Michael is presently at pail 0 and the garbage truck is at pail 1 . Michael takes seconds to walk between pails, so for he passes pail after seconds. The truck takes 20 seconds to travel between pails and stops for 30 seconds at each pail. Thus for it leaves pail after seconds, and for it arrives at pail after seconds. Michael will meet the truck at pail if and only if
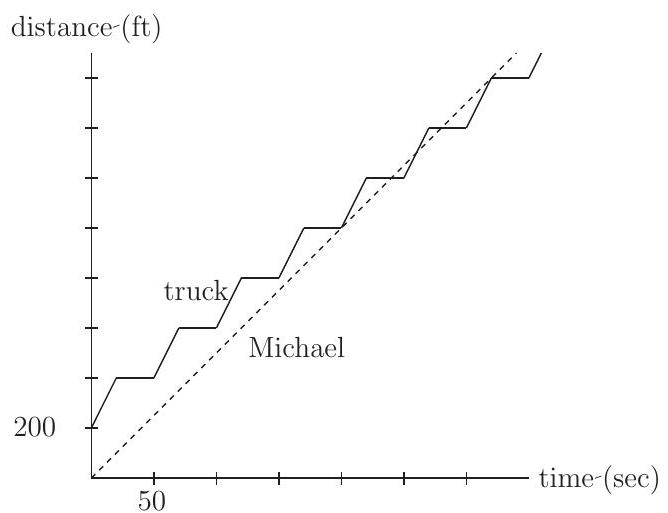
Hence Michael first meets the truck at pail 5 after 200 seconds, just as the truck leaves the pail. He passes the truck at pail 6 after 240 seconds and at pail 7 after 280 seconds. Finally, Michael meets the truck just as it arrives at pail 8 after 320 seconds. These conditions imply that the truck is ahead of Michael between pails 5 and 6 and that Michael is ahead of the truck between pails 7 and 8. However, the truck must pass Michael at some point between pails 6 and 7 , so they meet a total of times.
The problems on this page are the property of the MAA's American Mathematics Competitions