Problem:
Let S be the square one of whose diagonals has endpoints (0.1,0.7) and (−0.1,−0.7). A point v=(x,y) is chosen uniformly at random over all pairs of real numbers x and y such that 0≤x≤2012 and 0≤y≤2012. Let T(v) be a translated copy of S centered at v. What is the probability that the square region determined by T(v) contains exactly two points with integer coordinates in its interior?
Answer Choices:
A. 0.125
B. 0.14
C. 0.16
D. 0.25
E. 0.32
Solution:
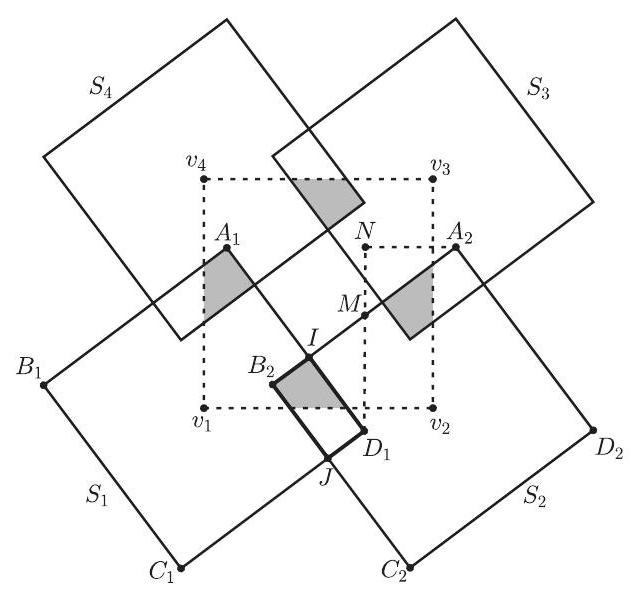
Consider the unit square U with vertices v1=(0,0),v2= (1,0),v3=(1,1), and v4=(0,1), and the squares Si=T(vi) with i=1,2,3,4. Note that T(v) contains vi if and only if v∈Si. First choose a point v=(x,y) uniformly at random over all pairs of real numbers (x,y) such that 0≤x≤1 and 0≤y≤1. In this case, the probability that T(v) contains vi and vj is the
area of the intersection of the squares U,Si, and Sj. This intersection is empty when vivj is a diagonal of U and it is equal to Area (U∩Si∩Sj) when vivj is a side of U. By symmetry, the probability that T(v) contains two vertices of U is 4 - Area (U∩S1∩S2)=2. Area (S1∩S2). By periodicity, this probability is the same as when the point v=(x,y) is chosen uniformly at random over all pairs of real numbers (x,y) such that 0≤x≤2012 and 0≤y≤2012.
For i=1 and 2 , let Ai,Bi,Ci, and Di be the vertices of Si in counterclockwise order, where A1=(0.1,0.7) and A2=(1.1,0.7). Then B2=(0.3,0.1) and D1= (0.7,−0.1). Let M=(0.7,0.4) be the midpoint of A2B2 and N=(0.7,0.7). Let I∈A2B2 and J∈C1D1 be the points of intersection of the boundaries of S1 and S2. Then S1∩S2 is the rectangle IB2JD1. Because D1,M, and N are collinear and D1M=MA2=0.5, the right triangles A2NM and D1IM are congruent. Hence ID1=NA2=1.1−0.7=0.4 and IB2=MB2−MI=MB2−MN= 0.5−0.3=0.2. Therefore Area (S1∩S2)=Area(IB2JD1)=0.2⋅0.4=0.08, and thus the required probability is 0.16 .
The problems on this page are the property of the MAA's American Mathematics Competitions