Problem:
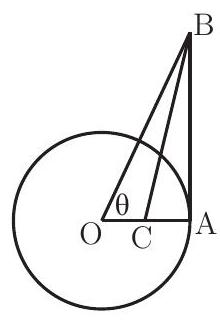
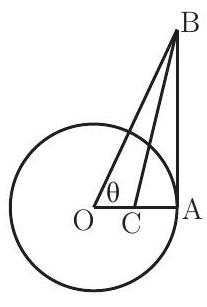
A circle centered at O has radius 1 and contains the point A. Segment AB is tangent to the circle at A and ∠AOB=θ. If point C lies on OA and BC bisects ∠ABO, then OC=
Answer Choices:
A. sec2θ−tanθ
B. 21
C. 1+sinθcos2θ
D. 1+sinθ1
E. cos2θsinθ
Solution:
The fact that OA=1 implies that BA=tanθ and BO=secθ. Since BC bisects ∠ABP, it follows that BAOB=CAOC, which implies OB+BAOB=OC+CAOC=OC. Substituting yields
OC=secθ+tanθsecθ=1+sinθ1
OR
Let α=∠CBO=∠ABC. Using the Law of Sines on triangle BCO yields BCsinθ=OCsinα, so OC=sinθBCsinα. In right triangle ABC,sinα=BC1−OC. Hence OC=sinθ1−OC. Solving this for OC yields OC=1+sinθ1.
The problems on this page are the property of the MAA's American Mathematics Competitions