Problem:
How many ordered pairs of real numbers satisfy the following system of equations?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The graph of the system is shown below.
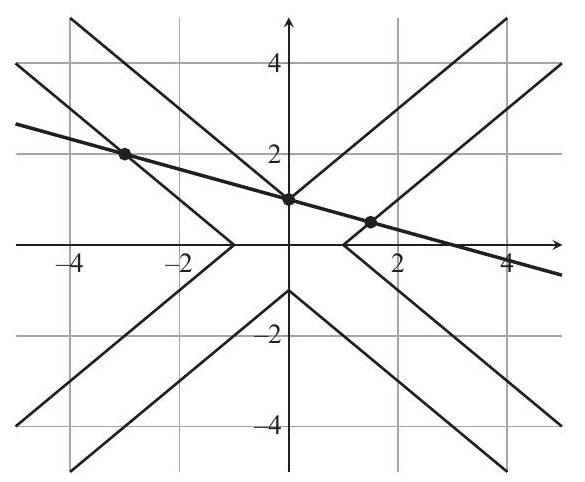
The graph of the first equation is a line with $x$-intercept $(3,0)$ and $y$-intercept $(0,1)$. To draw the graph of the second equation, consider the equation quadrant by quadrant. In the first quadrant $x>0$ and $y>0$, and thus the second equation is equivalent to $|x-y|=1$, which in turn is equivalent to $y=x \pm 1$. Its graph consists of the rays with endpoints $(0,1)$ and $(1,0)$, as shown. In the second quadrant $x<0$ and $y>0$. The corresponding graph is the reflection of the first quadrant graph across the $y$-axis. The rest of the graph can be sketched by further reflections of the first-quadrant graph across the coordinate axes, resulting in the figure shown. There are 3 intersection points: $(-3,2),(0,1)$, and $\(\left({\dfrac{3}{2}}, {\dfrac{1}{2}}\right)\)$ as shown.
OR
The second equation implies that or . There are four cases:
-
If , then , so .
-
If , then , so .
-
If , then , so again .
-
If , then , so .
It may be checked that each of these ordered pairs actually satisfies the given equations, so the total number of solutions is .
The problems on this page are the property of the MAA's American Mathematics Competitions