Problem:
Distinct planes intersect the interior of a cube . Let be the union of the faces of and let . The intersection of and consists of the union of all segments joining the midpoints of every pair of edges belonging to the same face of . What is the difference between the maximum and the minimum possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
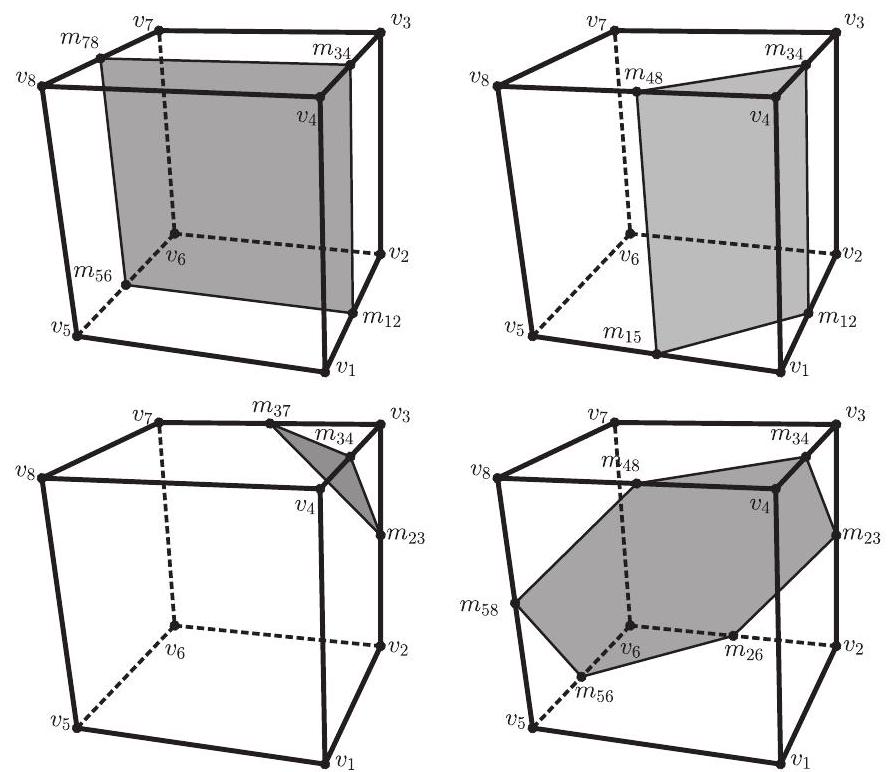
Label the vertices of as in the figure. Let denote the midpoint of . Call a segment long if it joins midpoints of opposite edges of a face and short if it joins midpoints of adjacent edges.
Let be one of the planes. Assume intersects the face . First suppose intersects by a long segment. By symmetry assume . Because intersects the interior of , it follows that intersects the face . By symmetry there are two cases: and .
In Case 1.1 the plane is the plane determined by the square . Note that contains 4 long segments and by symmetry there are 3 planes like , one for every pair of opposite faces of .
In Case 1.2 the plane is determined by the rectangle . Note that contains 2 long segments and 2 short segments, and by symmetry there are 12 planes like , one for every edge of .
Second, suppose intersects by a short segment. By symmetry assume . Again must intersect the face . There are three cases: , and 2.3 .
In Case 2.1 the plane is the plane determined by the triangle . Note that contains 3 short segments and by symmetry there are 8 planes like , one for every vertex of .
Case 2.2 duplicates Case 1.2.
In Case 2.3 the plane is determined by the hexagon . Note that contains 6 short segments, and by symmetry there are 4 planes like , one for every pair of opposite vertices of .
Therefore the maximum possible value of is , obtained by considering all possible planes classified so far.
To find the minimum, note that consists of 24 short segments and 12 long segments. Every plane can contain at most 6 short segments; moreover, the union of the 4 planes obtained from Case 2.3 contains all 24 short segments. Similarly, every plane can contain at most 4 long segments; moreover, the union of the 3 planes obtained from Case 1.1 contains all 12 long segments. Thus the minimum possible value of is , and the required difference is .
The problems on this page are the property of the MAA's American Mathematics Competitions