Problem:
A circle centered at with a radius of 1 and a circle centered at with a radius of 4 are externally tangent. A third circle is tangent to the first two and to one of their common external tangents as shown. The radius of the third circle is
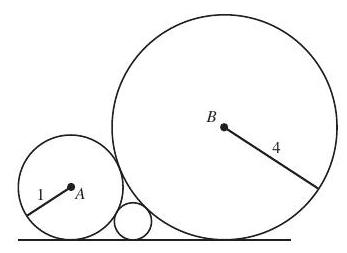
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the intersection of the horizontal line through and the vertical line through . In right triangle , we have and , so . Let be the radius of the third circle, and be the center. Let and be the points of intersection of the horizontal line through with the vertical lines through
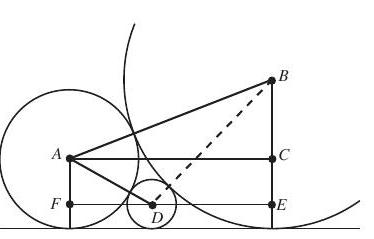
In we have and , so
and . In we have and , so
and . Hence,
and , which implies .
The problems on this page are the property of the MAA's American Mathematics Competitions