Problem:
A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
At each vertex there are three possible locations that the bug can travel to in the next move, so the probability that the bug will visit three different vertices after two moves is . Label the first three vertices that the bug visits as , and , in that order. In order to visit every vertex, the bug must travel from to either or .
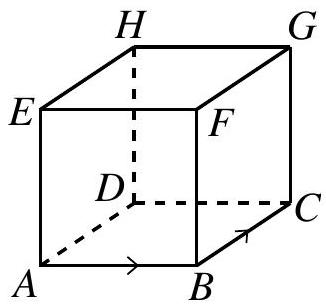
The bug travels to with probability , and from there the bug must visit the vertices , and in that order. Each of these choices has probability of occurring. So the probability that the path continues in the form
is .
Alternatively, the bug can travel from to and then from to . Each of these occurs with probability . From the bug could go either to or to , with probability , and from there to the two remaining vertices, each with probability . So the probability that the path continues in one of the forms
is .
Hence the bug will visit every vertex in seven moves with probability
OR
From a given starting point there are possible walks of seven moves for the bug, all of them equally likely. If such a walk visits every vertex exactly once,\
there are three choices for the first move and, excluding a return to the start, two choices for the second. Label the first three vertices visited as , and , in that order, and label the other vertices as shown. The bug must go to either or on its third move. In the first case it must then visit vertices , and in order. In the second case it must visit either , and or , and in order. Thus there are walks that visit every vertex exactly once, so the required probability is .
The problems on this page are the property of the MAA's American Mathematics Competitions