Problem:
Circles C1 and C2 each have radius 1 , and the distance between their centers is 21. Circle C3 is the largest circle internally tangent to both C1 and C2. Circle C4 is internally tangent to both C1 and C2 and externally tangent to C3. What is the radius of C4?
Answer Choices:
A. 141
B. 121
C. 101
D. 283
E. 91
Solution:
Let r be the radius of C4. Let the point Pk be the center of Ck for 1≤k≤4. Let A be the point of intersection of circles C1 and C4 and let ℓ be the tangent line to P1 at A. By symmetry, P3 is the midpoint of P1P2, and P1P3=41. Also by symmetry, P4 lies on the perpendicular bisector of P1P2. The radius P1A is perpendicular to ℓ. Likewise the radius P4A is perpendicular to ℓ, so P1,P4, and A all lie on the segment P1A with P4 between P1 and A. Then P1P4=1−r.
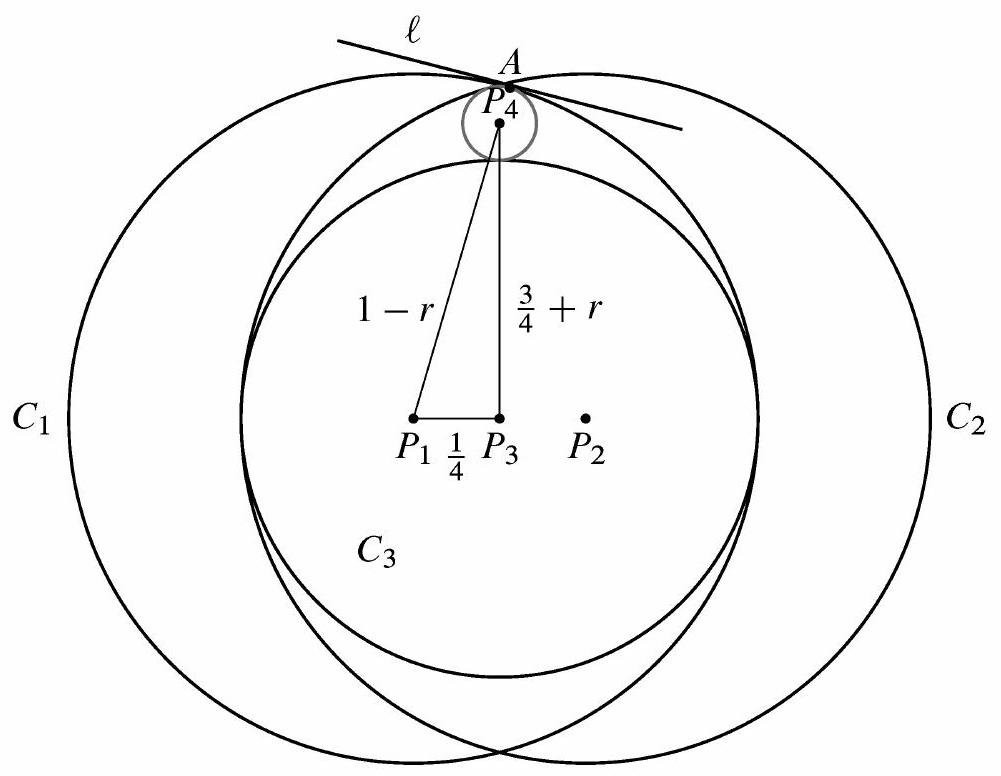
The radius of C3 is 43. Then P3P4=43+r, and △P1P3P4 is a right triangle with P1P3=41, P3P4=43+r, and P1P4=1−r. By the Pythagorean Theorem,
(41)2+(43+r)2=(1−r)2
Expanding gives
161+169+23r+r2=1−2r+r2
which gives r=(D)283.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)
