Problem:
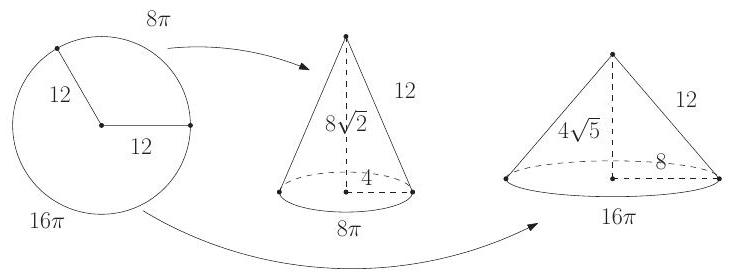
Jesse cuts a circular paper disk of radius 12 along two radii to form two sectors, the smaller having a central angle of 120 degrees. He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Each sector forms a cone with slant height 12. The circumference of the base of the smaller cone is . Hence the radius of the base of the smaller cone is 4 and its height is . Similarly, the circumference of the base of the larger cone is . Hence the radius of the base of the larger cone is 8 and its height is . The ratio of the volume of the smaller cone to the volume of larger cone is
The problems on this page are the property of the MAA's American Mathematics Competitions