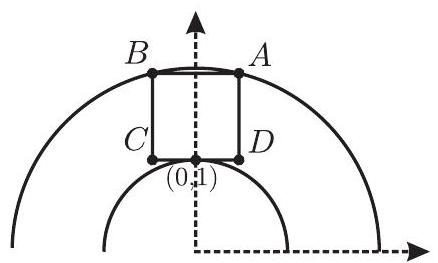
Problem:
A square region is externally tangent to the circle with equation 1 at the point on the side . Vertices and are on the circle with equation . What is the side length of this square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Suppose by symmetry that with . Because is tangent to the circle with equation at and both and are on the concentric circle with equation , it follows that . Then the horizontal length of the square is and its vertical height is . Therefore , or . Substituting this into the equation leads to the equation . By the quadratic formula, the positive root is , and so the side length is .
The problems on this page are the property of the MAA's American Mathematics Competitions