Problem:
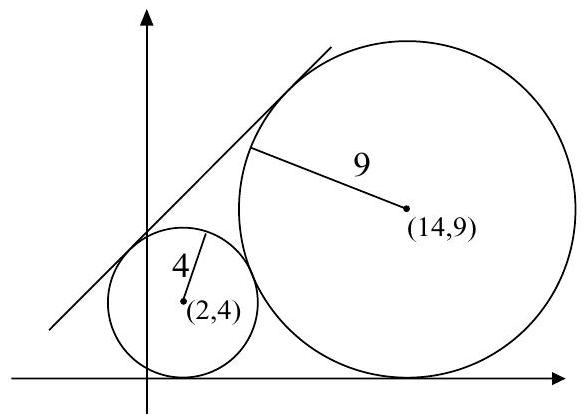
Circles with centers and have radii 4 and 9 , respectively. The equation of a common external tangent to the circles can be written in the form with . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The slope of the line containing the centers of the circles is , where is the acute angle between the -axis and line . The equation of line is . This line and the two common external tangents are concurrent. Because one of these tangents is the -axis, the point of intersection is the -intercept of line , which is . The acute angle between the -axis and the other tangent is , so the slope of that tangent is
Thus the equation of that tangent is , and
The problems on this page are the property of the MAA's American Mathematics Competitions