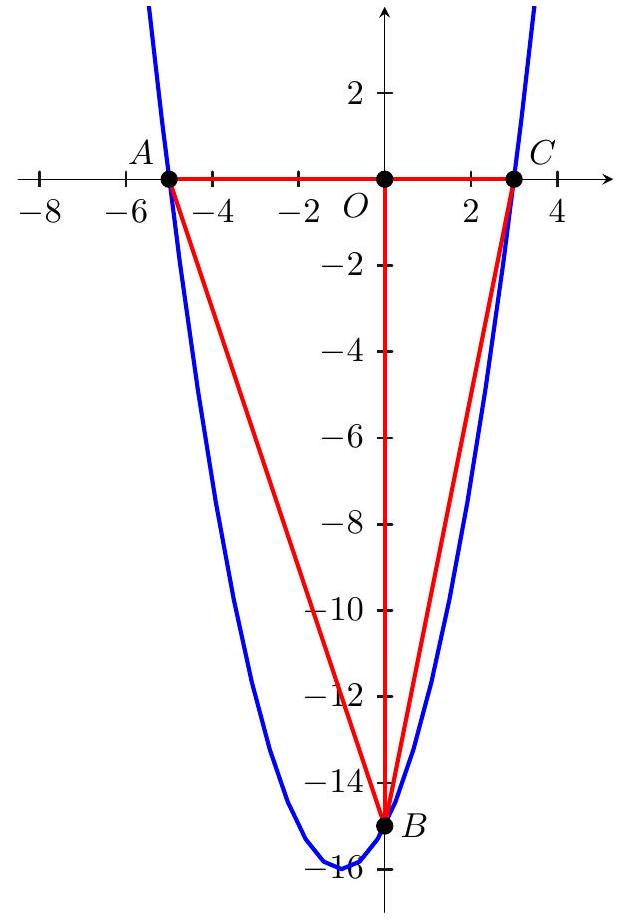
Problem: y = x 2 + 2 x − 15 y = x 2 + 2 x − 1 5 x x A A C C y y B B tan ( ∠ A B C ) tan ( ∠ A B C )
Answer Choices:
A. 1 7 7 1 1 4 4 1 3 7 7 3 1 2 2 1 4 7 7 4 Solution:
Let O O y = ( x + 5 ) ( x − 3 ) y = ( x + 5 ) ( x − 3 ) A = ( − 5 , 0 ) A = ( − 5 , 0 ) C = ( 3 , 0 ) C = ( 3 , 0 ) B B y y ( 0 , − 15 ) ( 0 , − 1 5 ) B O ‾ B O △ A B C △ A B C
tan ( ∠ A B C ) = tan ( ∠ A B O + ∠ O B C ) = tan ( ∠ A B O ) + tan ( ∠ O B C ) 1 − tan ( ∠ A B O ) ⋅ tan ( ∠ O B C ) = 5 15 + 3 15 1 − 5 15 ⋅ 3 15 = 8 15 − 1 = ( E ) 4 7 . tan ( ∠ A B C ) = tan ( ∠ A B O + ∠ O B C ) = 1 − tan ( ∠ A B O ) ⋅ tan ( ∠ O B C ) tan ( ∠ A B O ) + tan ( ∠ O B C ) = 1 − 1 5 5 ⋅ 1 5 3 1 5 5 + 1 5 3 = 1 5 − 1 8 = ( E ) 7 4 .
OR OR
With the notation as above,
A B = ( − 5 − 0 ) 2 + ( 0 − ( − 15 ) 2 = 250 , B C = ( 0 − 3 ) 2 + ( − 15 − 0 ) 2 = 234 , A B = ( − 5 − 0 ) 2 + ( 0 − ( − 1 5 ) 2 = 2 5 0 , B C = ( 0 − 3 ) 2 + ( − 1 5 − 0 ) 2 = 2 3 4 ,
and A C = ∣ − 5 − 3 ∣ = 8 A C = ∣ − 5 − 3 ∣ = 8 △ A B C △ A B C
cos ( ∠ A B C ) = 250 + 234 − 64 2 ⋅ 250 ⋅ 234 = 7 65 . cos ( ∠ A B C ) = 2 ⋅ 2 5 0 ⋅ 2 3 4 2 5 0 + 2 3 4 − 6 4 = 6 5 7 .
Therefore 2 ( ∠ A B C ) = 49 65 cos 2 ( ∠ A B C ) = 6 5 4 9
2 ( ∠ A B C ) = 1 − 2 ( ∠ A B C ) = 16 65 sin 2 ( ∠ A B C ) = 1 − cos 2 ( ∠ A B C ) = 6 5 1 6
so 2 ( ∠ A B C ) = 16 49 tan 2 ( ∠ A B C ) = 4 9 1 6 ∠ A B C ∠ A B C 16 49 = ( E ) 4 7 4 9 1 6 = ( E ) 7 4
The problems on this page are the property of the MAA's American Mathematics Competitions