Problem:
Rhombus ABCD has side length 2 and ∠B=120∘. Region R consists of all points inside the rhombus that are closer to vertex B than any of the other three vertices. What is the area of R ?
Answer Choices:
A. 33​​
B. 23​​
C. 323​​
D. 1+33​​
E. 2 Solution:
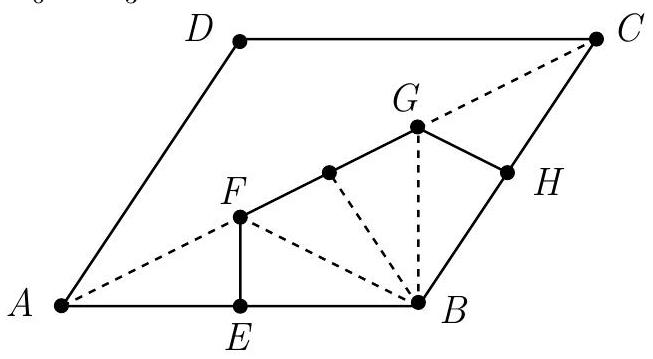
Let E and H be the midpoints of AB and BC, respectively. The line drawn perpendicular to AB through E divides the rhombus into two regions: points that are closer to vertex A than B, and points that are closer to vertex B than A. Let F be the intersection of this line with diagonal AC. Similarly, let point G be the intersection of the diagonal AC with the perpendicular to BC drawn from H. Then the desired region R is the pentagon BEFGH.
Note that △AFE is a 30−60−90∘ triangle with AE=1. Hence the area of △AFE is 21​⋅1⋅3​1​=63​​. Both △BFE and △BGH are congruent to △AFE, so they have the same areas. Also ∠FBG=120∘−∠FBE−∠GBH=\ 60∘, so △FBG is an equilateral triangle. In fact, the altitude from B to FG divides △FBG into two triangles, each congruent to △AFE. Hence the area of BEFGH is 4⋅63​​=323​​​.
