Problem:
Real numbers and are chosen independently and uniformly at random from the interval . What is the probability that , where denotes the greatest integer less than or equal to the real number ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The set of all possible ordered pairs is bounded by the unit square in the coordinate plane with vertices , , and . For each positive integer if and only if and . Thus the set of ordered pairs such that is bounded by a square with side length and therefore area . The union of these squares over all positive integers has area
and therefore the requested probability is . (It is also clear from the diagram that one third of the square is shaded.)
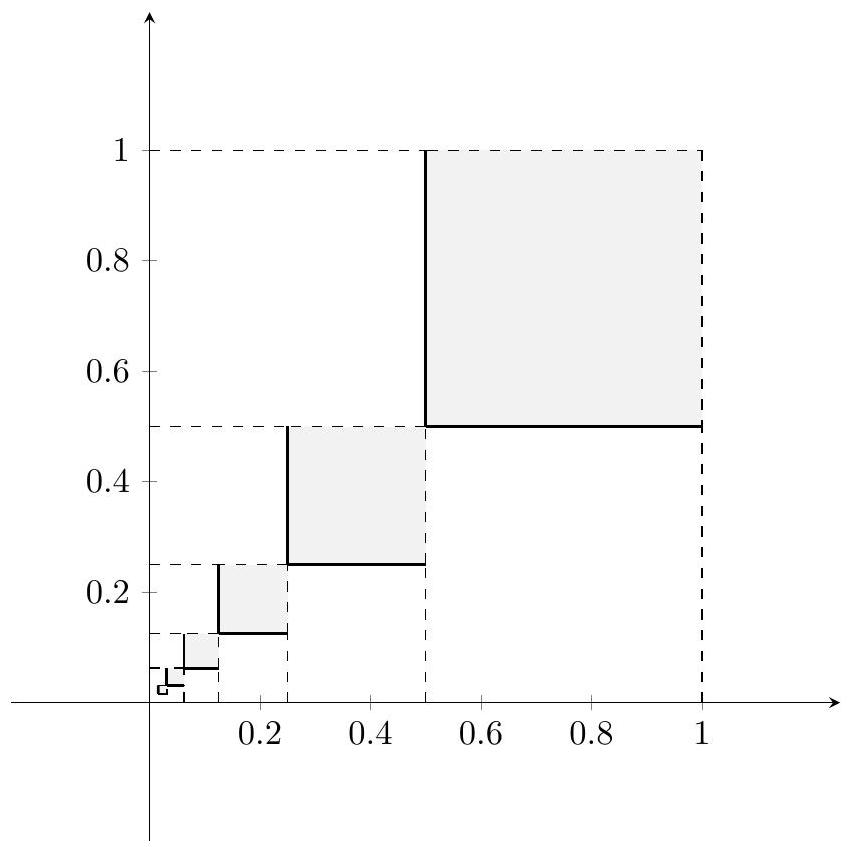
OR
The problem can be modeled with Xerxes and Yolanda each repeatedly flipping a fair coin to determine the binary (base two "decimal") expansions of and , respectively. If Xerxes flips a head, he writes down a 0 as the next binary digit; if he flips a tail, he writes down a 1. Yolanda does the same. Then if and only if the first time that either of them flips a tail, so does the other. There
are three equally likely outcomes: tail-tail, tail-head, and head-tail. Therefore the requested probability is .
The problems on this page are the property of the MAA's American Mathematics Competitions